Chọn phương án đúng trong mỗi câu sau:
Câu 1
Cho đường thẳng a và một điểm O cách a một khoảng bằng 6cm. Khẳng định nào sau đây là đúng về vị trí tương đối của đường thẳng a và đường tròn (O; 9cm)?
A. Đường thẳng a cắt đường tròn (O) tại hai điểm.
B. Đường thẳng a tiếp xúc với đường tròn (O).
C. Đường thẳng a và đường tròn (O) không có điểm chung.
D. Đường thẳng a và đường tròn (O) có duy nhất điểm chung.

Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:
+ Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d
+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\).
+ Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\).

Vì \(6cm
Chọn A
Câu 2
Cho một điểm M nằm ngoài đường tròn (I; 6cm), vẽ tiếp tuyến MB đến đường tròn đó (B là tiếp điểm). Nếu \(MI = 10cm\) thì độ dài MB bằng
A. 6 cm.
B. 8 cm.
C. 7 cm.
D. 10 cm.

+ Chứng minh tam giác MBI vuông tại B.
+ Áp dụng định lý Pythagore vào tam giác MBI vuông tại B ta tính được MB.

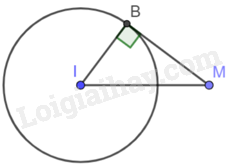
Vì MB là tiếp tuyến của (I) nên \(MB \bot IB\) tại B. Khi đó tam giác IMB vuông tại B.
Áp dụng định lý Pythagore vào tam giác MBI vuông tại B ta có:
\(I{B^2} + M{B^2} = M{I^2}\)
\(MB = \sqrt {M{I^2} - I{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\left( {cm} \right)\)
Chọn B
Câu 3
Cho đường thẳng a và một điểm O cách a là 3cm. Vẽ đường tròn (O; 5cm). Gọi B, C là các giao điểm của đường thẳng a và (O). Diện tích của tam giác OBC bằng
Advertisements (Quảng cáo)
A. \(10c{m^2}\).
B. \(6c{m^2}\).
C. \(24c{m^2}\).
D. \(12c{m^2}\).

+ Qua O kẻ đường thẳng vuông góc với BC tại H. Khi đó, OH là khoảng cách từ O đến đường thẳng a. Do đó, \(OH = 3cm\).
+ Chứng minh tam giác OBC cân tại O, suy ra OH là đường trung tuyến, suy ra \(BH = HC = \frac{1}{2}BC\).
+ Áp dụng định lý Pythagore vào tam giác BOH vuông tại H tính được BH, từ đó tính được BC.
+ Diện tích tam giác OBC là: \(S = \frac{1}{2}OH.BC\)

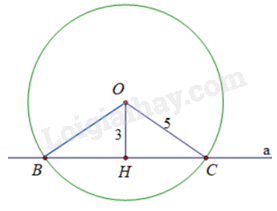
Qua O kẻ đường thẳng vuông góc với BC tại H. Khi đó, OH là khoảng cách từ O đến đường thẳng a. Do đó, \(OH = 3cm\).
Tam giác OBC có: \(OB = OC\) (bán kính (O)) nên tam giác BOC cân tại O. Do đó, OH là đường cao đồng thời là đường trung tuyến của tam giác OBC. Suy ra \(BH = HC = \frac{1}{2}BC\).
Áp dụng định lý Pythagore vào tam giác BOH vuông tại H có:
\(O{H^2} + B{H^2} = O{B^2}\) nên \(BH = \sqrt {B{O^2} - O{H^2}} = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right)\) nên \(BC = 2BH = 2.4 = 8\left( {cm} \right)\)
Diện tích tam giác OBC là: \(S = \frac{1}{2}OH.BC = \frac{1}{2}.3.8 = 12\left( {c{m^2}} \right)\)
Chọn D
Câu 4
Cho đường tròn (O) và điểm M nằm ngoài đường tròn, vẽ hai tiếp tuyến MA và MB của đường tròn (O). Biết \(\widehat {AMB} = {35^o}\). Số đo cung nhỏ AB là
A. \({145^o}\).
B. \({215^o}\).
C. \({125^o}\).
D. \({235^o}\).

+ Chứng minh \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
+ Tứ giác \(\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}\), từ đó tính được góc AOB, suy ra số đo cung nhỏ AB.

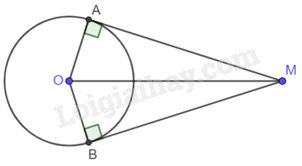
Vì MA, MB là tiếp tuyến của đường tròn (O) nên \(MA \bot OA,MB \bot OB\) nên \(\widehat {MAO} = \widehat {MBO} = {90^o}\).
Tứ giác MBOA có: \(\widehat {MAO} + \widehat {MBO} + \widehat {AMB} + \widehat {AOB} = {360^o}\)
\(\widehat {AOB} = {360^o} - \widehat {MAO} - \widehat {MBO} - \widehat {AMB} = {360^o} - {90^o} - {90^o} - {35^o} = {145^o}\)
Vì góc ở tâm AOB chắn cung nhỏ AB nên số đo cung nhỏ AB bằng \({145^o}\).
Chọn A
