
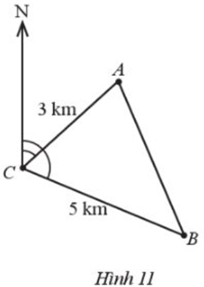
Tàu A cách cảng C một khoảng 3 km và lệch hướng bắc một góc 47,450. Tàu B cách cảng C một khoảng 5 km và lệch hướng bắc một góc 112,900 (Hình 11). Hỏi khoảng cách giữa hai tàu là bao nhiêu kilomet (làm tròn kết quả đến hàng phần trăm)?

Bước 1: Từ giả thiết xác định số đo các góc \(\widehat {NCA},\widehat {NCB},\widehat {ACB}\)
Bước 2: Áp dụng định lí cosin cho ∆ABC để tính độ dài AB rồi kết luận

Advertisements (Quảng cáo)
Theo giả thiết,
\(\widehat {NCA} = 47,{45^0},\widehat {NCB} = 112,{90^0} \Rightarrow \widehat {ACB} = \widehat {NCB} - \widehat {NCA} = 65,{45^0}\)
Áp dụng định lí cosin cho ∆ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}\)
\( \Rightarrow AB = \sqrt {A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}} \)
\( = \sqrt {{3^2} + {5^2} - 2.3.5.\cos 65,{{45}^0}} \approx 4,64\)
Vậy khoảng cách giữa hai tàu là 4,64 km
