
Giá trị lớn nhất của biểu thức \(F\left( {x;y} \right) = 3x + y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{x + y \le 2}\\{y \ge 0}\end{array}} \right.\) là:
A. -3.
B. 6.
C. 5.
D. 8.

- Vẽ các bất phương trình trên cùng một mặt phẳng tọa độ \(Oxy.\)
- Xác định miền nghiệm của hệ bất phương trình trên.
- Tìm giá trị lớn nhất của biểu thức dựa trên miền nghiệm vừa tìm được.
Advertisements (Quảng cáo)

Miền nghiệm của bất phương trình \(x \ge - 1\) là nửa mặt phẳng bờ \(d:x = - 1\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(x + y \le 2\) là nửa mặt phẳng bờ \({d_1}:x + y = 2\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \({d_2}:y = 0\) chứa điểm \(\left( {0;1} \right).\)
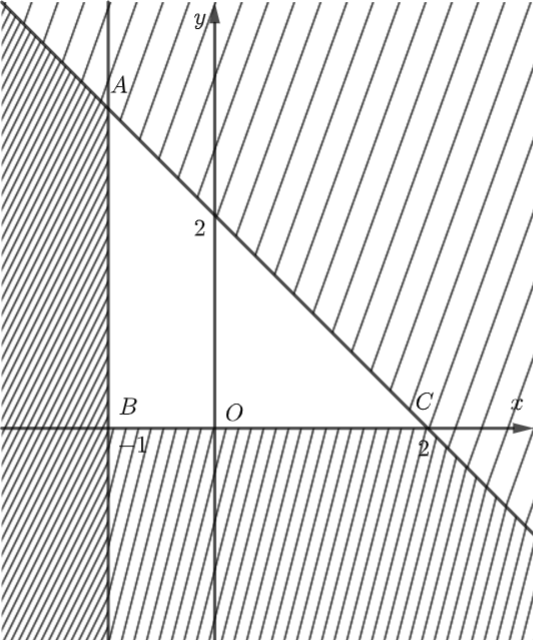
Miền nghiệm của hệ bất phương trình trên là tam giác \(ABC\) với \(A\left( { - 1;3} \right),\) \(B\left( { - 1;0} \right),\) \(C\left( {2;0} \right).\)
Ta có: \(F\left( { - 1;3} \right) = 3\left( { - 1} \right) + 3 = 0,\,\,F\left( { - 1;0} \right) = 3\left( { - 1} \right) + 0 = - 3,\,\,F\left( {2;0} \right) = 3.2 + 0 = 6.\)
Vậy giá trị lớn nhất của \(F\) là \(F\left( {2;0} \right) = 6.\)
Chọn B.
