
Tổng các giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = x + 5y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{ - 2 \le y \le 2}\\{x + y \le 4}\\{y - x \le 4}\end{array}} \right.\) là:
A. \( - 20.\)
B. \(-4.\)
C. \(28.\)
D. \( 16.\)

- Vẽ các bất phương trình trên cùng một mặt phẳng tọa độ \(Oxy.\)
- Xác định miền nghiệm của bất phương trình trên.
- Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức dựa vào miền nghiệm vừa xác định được.

Advertisements (Quảng cáo)
Miền nghiệm của bất phương trình \( - 2 \le y \le 2\) là miền nằm giữa hai đường thẳng \(d:y = - 2\) và \({d_1}:y = 2\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(x + y \le 4\) là nửa mặt phẳng bờ \({d_2}:x + y = 4\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(y - x \le 4\) là nửa mặt phẳng bờ \({d_3}:y - x = 4\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
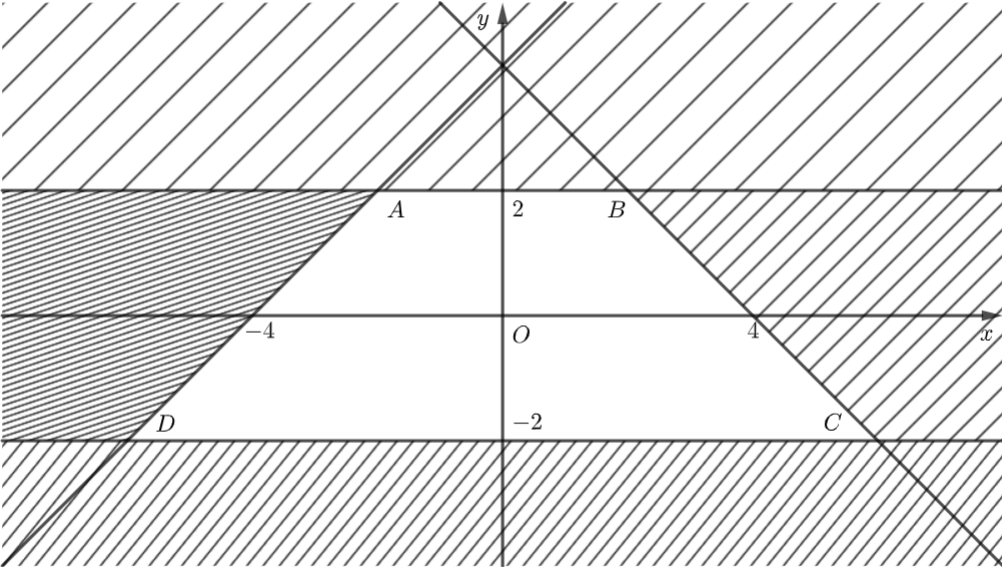
Miền nghiệm của hệ bất phương trình trên là hình thang cân \(ABCD\) với \(A\left( { - 2;2} \right),\) \(B\left( {2;2} \right),\) \(C\left( {6; - 2} \right),\) \(D\left( { - 6; - 2} \right).\)
Ta có: \(F\left( { - 2;2} \right) = - 2 + 5.2 = 8,\,\,F\left( {2;2} \right) = 2 + 5.2 = 12,\)
\(F\left( {6; - 2} \right) = 6 + 5\left( { - 2} \right) = - 4,\,\,F\left( { - 6; - 2} \right) = - 6 + 5\left( { - 2} \right) = - 16.\)
\( \Rightarrow \) giá trị lớn nhất của \(F\) là: \(F\left( {2;2} \right) = 12,\) giá trị nhỏ nhất của \(F\) là: \(F\left( { - 6; - 2} \right) = - 16.\)
Tổng giá trị lớn nhất và giá trị nhỏ nhất của \(F\) là: \(12 + \left( { - 16} \right) = - 4.\)
Chọn B.
