
Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc \(X\) và gia súc \(Y\) để tạo thành thức ăn hỗn hợp cho gia súc. Giá một bao loại \(X\) là 250 nghìn đồng, giá một bao loại \(Y\) là 200 nghìn đồng. Mỗi bao loại \(X\) chứa 2 đơn vị chất dinh dưỡng A, 2 đơn vị chất dinh dưỡng B và 2 đơn vị chất dinh dưỡng C. Mỗi bao loại \(Y\) chứa 1 đơn vị chất dinh dưỡng A, 9 đơn vị chất dinh dưỡng B và 3 đơn vị chất dinh dưỡng C. Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc \(X\) và \(Y\) sao cho hỗn hợp thu được tối thiểu 12 đơn vị chất dinh dưỡng A, 36 đơn vị chất dinh dưỡng B và 24 đơn vị chất dinh dưỡng C.
A. \(1,95\) triệu đồng.
B. \(4,5\) triệu đồng.
C. \(1,85\) triệu đồng.
D. \(1,7\) triệu đồng.

- Viết hệ bất phương trình từ bài toán trên
- Xác định miền nghiệm của hệ bất phương trình đó
- Viết biểu thức biểu thị chi phí để mua hai loại thức ăn gia súc loại \(X\) và \(Y\)
- Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc loại \(X\) và \(Y\) từ miền nghiệm vừa tìm được.

- Gọi \(x\) và \(y\) lần lượt là số bao loại \(X\) và \(Y.\) Điều kiện: \(x \ge 0;\,\,y \ge 0.\)
Advertisements (Quảng cáo)
Số lượng chất dinh dưỡng A cần dùng để tạo thành hai loại thức ăn gia súc \(X\) và \(Y\) là: \(2x + y \ge 12.\)
Số lượng chất dinh dưỡng B cần dùng để tạo thành hai loại thức ăn gia súc \(X\) và \(Y\) là: \(2x + 9y \ge 36.\)
Số lượng chất dinh dưỡng C cần dùng để tạo thành hai loại thức ăn gia súc \(X\) và \(Y\) là: \(2x + 3y \ge 24.\)
Từ đó, ta có hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{2x + y \ge 12.}\\{2x + 9y \ge 36.}\\{2x + 3y \ge 24.}\end{array}} \right.\)
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ \(d:x = 0\) chứa điểm \(\left( {1;0} \right).\)
Miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \({d_1}:y = 0\) chứa điểm \(\left( {0;1} \right).\)
Miền nghiệm của bất phương trình \(2x + y \ge 12\) là nửa mặt phẳng bờ \({d_2}:2x + y = 12\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(2x + 9y \ge 36\) là nửa mặt phẳng bờ \({d_3}:2x + 9y = 36\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(2x + 3y \ge 24\) là nửa mặt phẳng bờ \({d_4}:2x + 3y = 24\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
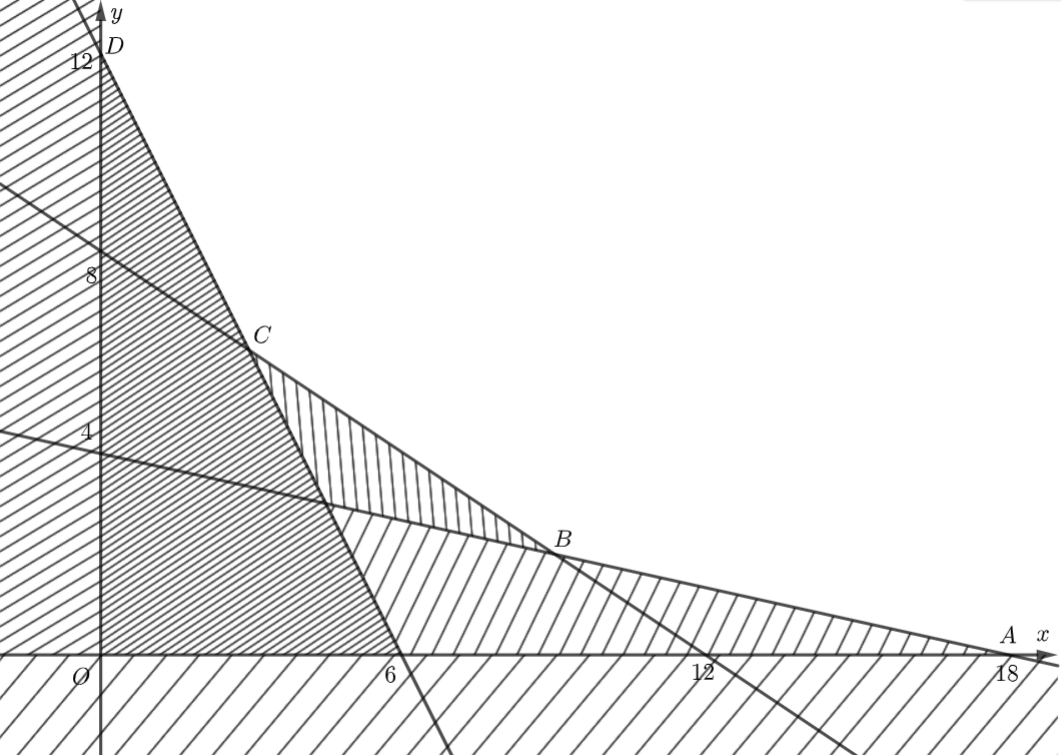
Miền nghiệm của hệ bất phương trình là: miền không bị gạch với các đỉnh \(A\left( {18;0} \right),\) \(B\left( {9;2} \right),\) \(C\left( {3;6} \right),\) \(D\left( {0;12} \right).\)
- Chi phí để mua hai loại thức ăn gia súc loại \(X\) và \(Y\) là: \(F\left( {x;y} \right) = 250x + 200y\) (nghìn đồng).
- Ta có: \(F\left( {18;0} \right) = 250.18 + 200.0 = 4500,\,\,F\left( {9;2} \right) = 250.9 + 200.2 = 2650,\)
\(F\left( {3;6} \right) = 250.3 + 200.6 = 1950,\,\,F\left( {0;12} \right) = 250.0 + 200.12 = 2400.\)
Vậy chi phí nhỏ nhất để mua hai loại thức ăn gia súc loại \(X\) và \(Y\) là: \(F\left( {3;6} \right) = 1950.\)
Chọn A.
