Một xí nghiệp sản xuất hai loại sản phẩm kí hiệu là \(I\) và \(II\). Một tấn sản phẩm \(I\) lãi 2 triệu đồng, một tấn sản phẩm \(II\) lãi 1,6 triệu đồng. Muốn sản xuất 1 tấn sản phẩm \(I\) phải dùng máy \(M_1\) trong 3 giờ và máy \(M_2\) trong 1 giờ. Muốn sản xuất 1 tấn sản phẩm \(II\) phải dùng máy \(M_1\) trong 1 giờ và máy \(M_2\) trong 1 giờ. Biết rằng một máy không thể dùng để sản xuất đồng ngày, máy \(M_2\) một ngày chỉ làm việc không quá 4 giờ.
Giả sử xí nghiệp sản xuất trong một ngày được \(x\) (tấn) sản phẩm \(I\) và \(y\) (tấn) sản phẩm \(II\).
a. Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm (S) của hệ đó.
b. Gọi T (triệu đồng) là số tiền lãi mỗi ngày của xí nghiệp. Hãy biểu diễn T theo \(x, y\).
c. Ở câu a) ta thấy (S) là một miền đa giác. Biết rằng T có giá trị lớn nhất tại \((x_0 ; y_0)\) với \((x_0 ; y_0)\) là tọa độ của một trong các đỉnh của (S).
Hãy đặt kế hoạch sản xuất của xí nghiệp sao cho tổng số tiền lãi cao nhất.
 :
:
a. Số giờ làm việc trong mỗi ngày của \(M_1\) là \(3x + y\).
Số giờ làm việc trong mỗi ngày của \(M_2\) là \(x + y\).
Advertisements (Quảng cáo)
Theo bài ra ta có hệ bất phương trình
\(\left( I \right)\left\{ {\begin{array}{*{20}{c}}{3x + y \le 6}\\{x + y \le 4}\\{x \ge 0}\\{y \ge 0.}\end{array}} \right.\)
Miền nghiệm (S) của hệ (I) là miền tứ giác OABC (h.4.13).
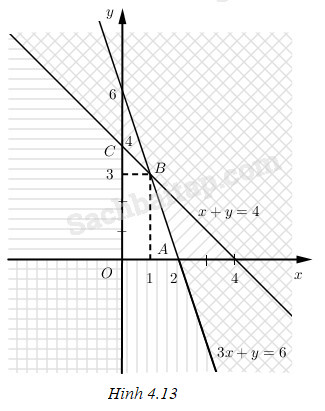
b. Số tiền lãi của xí nghiệp mỗi ngày là \(T = 2x + 1,6y\) (triệu đồng)
c. \(T = 2x + 1,6y\) đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác OABC. Dùng phép thử trực tiếp, ta thấy \(T = 2x + 1,6y\) đạt giá trị lớn nhất khi \(x = 1 ; y = 3\) (điểm B).
Vậy để số tiền lãi lớn nhất (6,8 triệu đồng), xí nghiệp cần sản xuất mỗi ngày 1 tấn sản phẩm \(I\) và 3 tấn sản phẩm \(I\).
