Cho tứ giác ABCD.Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh rằng:
a) \(\overrightarrow {MN} = \overrightarrow {QP}\)
b) \(\overrightarrow {MP} = \overrightarrow {MN} + \overrightarrow {MQ} \)
Gợi ý làm bài
(Xem hình 1.76)
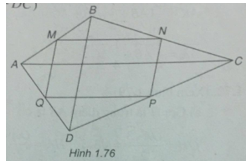
a) Ta có:
Advertisements (Quảng cáo)
\(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {BC} ) = {1 \over 2}\overrightarrow {AC} \)
\(\overrightarrow {QP} = \overrightarrow {QD} + \overrightarrow {DP} = {1 \over 2}(\overrightarrow {AD} + \overrightarrow {DC} ) = {1 \over 2}\overrightarrow {AC} \)
Suy ra \(\overrightarrow {MN} = \overrightarrow {QP}\)
b) Tứ giác MNPQ có: \(\left\{ \matrix{
MN{\rm{//}}QD \hfill \cr
MN = QP \hfill \cr} \right.\)
Suy ra MNPQ là hình bình hành.
Suy ra \(\overrightarrow {MP} = \overrightarrow {MN} + \overrightarrow {MQ} \)
