Advertisements (Quảng cáo)
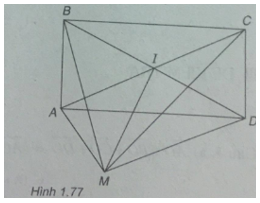
Cho hình chữ nhật ABCD. Gọi I là giao điểm của hai đường chéo AC và BD.
a) Với điểm M tùy ý, hãy chứng minh:
\(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
b) Chứng minh rằng: \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right|\)
Gợi ý làm bài
(Xem hình 1.77)
a) \(\overrightarrow {MA} + \overrightarrow {MC} = 2\overrightarrow {MI} \)
\(\overrightarrow {MB} + \overrightarrow {MD} = 2\overrightarrow {MI}\)
Vậy \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
b) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} = > \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = AC\)
\(\overrightarrow {AB} – \overrightarrow {AD} = \overrightarrow {DB} = > \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = DB\)
Vì hai đường chéo của hình chữ nhật dài bằng nhau nên
\(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right|\)