Giải bất phương trình sau:
\(|x + 2| + \left| { - 2x + 1} \right| \le x + 1\)
Gợi ý làm bài
Bỏ dấu giá trị tuyệt đối ở vế trái của bất phương trình ta có:
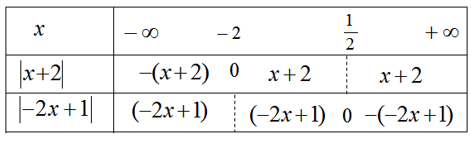
Advertisements (Quảng cáo)
Bất phương trình đã cho tương đương với
\(\eqalign{
& \left[ \matrix{
\left\{ \matrix{
x \le - 2 \hfill \cr
- (x + 2) + ( - 2x + 1) \le x + 1 \hfill \cr} \right. \hfill \cr
\left\{ \matrix{
- 1 < x \le {1 \over 2} \hfill \cr
(x + 2) + ( - 2x + 1) \le x + 1 \hfill \cr} \right. \hfill \cr
\left\{ \matrix{
x > {1 \over 2} \hfill \cr
(x + 2) - ( - 2x + 1) \le x + 1 \hfill \cr} \right. \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
\left\{ \matrix{
x \le - 2 \hfill \cr
4x \ge - 2 \hfill \cr} \right. \hfill \cr
\left\{ \matrix{
- 1 < x \le {1 \over 2} \hfill \cr
2x \ge 2 \hfill \cr} \right. \hfill \cr
\left\{ \matrix{
x \ge {1 \over 2} \hfill \cr
2x \le 0 \hfill \cr} \right. \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
\left\{ \matrix{
x \le - 2 \hfill \cr
x \ge - {1 \over 2} \hfill \cr} \right. \hfill \cr
\left\{ \matrix{
- 2 < x \le {1 \over 2} \hfill \cr
x \ge 1 \hfill \cr} \right. \hfill \cr
\left\{ \matrix{
x > {1 \over 2} \hfill \cr
x \le 0 \hfill \cr} \right. \hfill \cr} \right. \cr} \)
(Vô nghiệm)
Vậy bất phương trình đã cho vô nghiệm.
