Giải bất phương trình sau. Bài 33 trang 114 Sách bài tập (SBT) Toán Đại số 10 - Bài 3: Dấu của nhị thức bậc nhất
Giải bất phương trình sau:
\({1 \over {x - 1}} + {1 \over {x + 2}} > {1 \over {x - 2}}\)
Gợi ý làm bài
\({1 \over {x - 1}} + {1 \over {x + 2}} > {1 \over {x - 2}} \Leftrightarrow {{x + 2 + x - 1} \over {(x + 2)(x - 1)}} > {1 \over {x - 2}}\)
\( \Leftrightarrow {{(2x + 1)(x - 2) - (x - 1)(x + 2)} \over {(x - 1)(x + 2)(x - 2)}} > 0\)
Advertisements (Quảng cáo)
\( \Leftrightarrow {{{x^2} - 4x} \over {(x - 1)(x + 2)(x - 2)}} > 0\)
\( \Leftrightarrow {{x(x - 4)} \over {(x - 1)(x + 2)(x - 2)}} > 0(1)\)
Bảng xét dấu vế trái của (1)
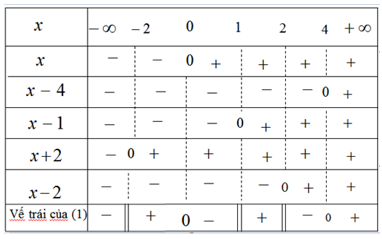
Đáp số: \( - 2 < x < 0;1 < x < 2;4 < x < + \infty \)
