Bài 7 trang 97 Toán 10 tập 1 – Chân trời sáng tạo: Cho tam giác ABC...

Cho tam giác ABC

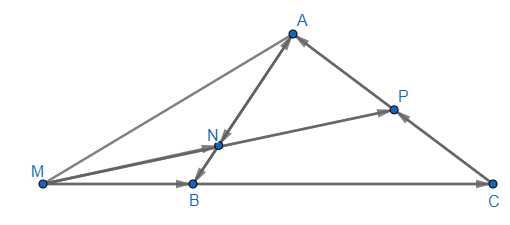
a)  Xác định các điểm M, N, P thỏa mãn: \(\overrightarrow {MB}  = \frac{1}{2}\overrightarrow {BC} ,\overrightarrow {AN}  = 3\overrightarrow {NB} ,\overrightarrow {CP}  = \overrightarrow {PA} \)

b) Biểu thị mỗi vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} \) theo hai vectơ \(\overrightarrow {BC} ,\overrightarrow {BA} \)

c) Chứng minh ba điểm M, N, P thẳng hàng

a)  Xác định hướng và tỉ số độ dài

\(\overrightarrow {MB}  = k.\overrightarrow {BC}  \Rightarrow \overrightarrow {MB} \) và \(\overrightarrow {BC} \) cùng hướng; tỉ số độ dài \(\frac{{BC}}{{MB}} = k\)

b)  Phân tích  \(\overrightarrow {MN}\) theo hai vecto \(\overrightarrow {MB}, \overrightarrow {NB}\)

c)  \(M,N,P\) thẳng hàng \( \Leftrightarrow \overrightarrow {MN}  = k.\overrightarrow {MP} \) \(\left( k \in {\mathbb Z}^* \right)\)

a)      Ta có:

+) \(\overrightarrow {MB}  = \dfrac{1}{2}\overrightarrow {BC}  \Rightarrow \overrightarrow {MB} \) và \(\overrightarrow {BC} \) cùng hướng; tỉ số độ dài \(\dfrac{{BC}}{{MB}} = 2\)

\( \Rightarrow M\) nằm ngoài đoạn thẳng BC sao cho \(MB = \dfrac{1}{2}BC\)

+) \({\overrightarrow {AN}  = 3\overrightarrow {NB}  \Rightarrow \overrightarrow {AB}  + \overrightarrow {BN}  = 3\overrightarrow {NB}  \Rightarrow 4\overrightarrow {NB}  = \overrightarrow {AB}  \Leftrightarrow \overrightarrow {NB}  = \dfrac{1}{4}\overrightarrow {AB} }\)

\( \Rightarrow N\) thuộc đoạn thẳng AB và \(NB=\dfrac{{1}}{{4}} AB\)

+) \(\overrightarrow {CP}  = \overrightarrow {PA}  \Leftrightarrow \overrightarrow {PC}  + \overrightarrow {PA}  = \overrightarrow 0 \)

\( \Rightarrow P\)là trung điểm của CA

b) \(\overrightarrow {MN}  = \overrightarrow {MB}  + \overrightarrow {BN}  = \frac{1}{2}\overrightarrow {BC}  + \frac{1}{4}\overrightarrow {BA} \)

\(\begin{array}{l}\overrightarrow {MP}  = \overrightarrow {MC}  + \overrightarrow {CP}  = \overrightarrow {MC}  + \frac{1}{2}\overrightarrow {CA}  \\= \frac{3}{2}\overrightarrow {BC}  + \frac{1}{2}\left( {\overrightarrow {BA}  - \overrightarrow {BC} } \right)\\ = \overrightarrow {BC}  + \frac{1}{2}\overrightarrow {BA} \end{array}\)

c) Ta có:

\(\overrightarrow {MN}  = \frac{1}{2}\overrightarrow {BC}  + \frac{1}{4}\overrightarrow {BA} ;\) \(\overrightarrow {MP}  = \overrightarrow {BC}  + \frac{1}{2}\overrightarrow {BA} \)

\( \Rightarrow \overrightarrow {MP}  = 2\overrightarrow {MN} \)

Vậy \(M,N,P\) thẳng hàng