Giải và biện luận các hệ phương trình
a)
\(\left\{ \matrix{
(m + 3)x + 2y = m \hfill \cr
(3m + 1)x + (m + 1)y = 1 \hfill \cr} \right.\)
b)
\(\left\{ \matrix{
(2m + 3)x + 5y = m - 11 \hfill \cr
(m + 2)x + 2y = m - 2 \hfill \cr} \right.\)
Đáp án
a) Ta có:
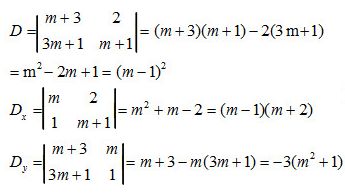
+ Nếu m ≠ 1 thì hệ có nghiệm (x, y) với:
Advertisements (Quảng cáo)
\(\eqalign{
& x = {{{D_x}} \over D} = {{(m - 1)(m + 2)} \over {{{(m - 1)}^2}}} = {{m + 2} \over {m - 1}} \cr
& y = {{{D_y}} \over D} = {{ - 3({m^2} - 1)} \over {{{(m - 1)}^2}}} = {{ - 3(m + 1)} \over {m - 1}} \cr} \)
+ Nếu m = 1 thì hệ thành
\(\left\{ \matrix{
4x + 2y = 1 \hfill \cr
4x + 2y = 1 \hfill \cr} \right. \Leftrightarrow y = - 2x + {1 \over 2}\)
Hệ có vô số nghiệm \((x,\, - 2x + {1 \over 2})\) với x ∈ R
b) Ta có:
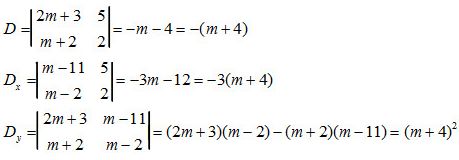
+Với \(m ≠ -4\) thì hệ có nghiệm (x, y) với:
\(\eqalign{
& x = {{{D_x}} \over D} = {{ - 3(m + 4)} \over { - (m + 4)}} = 3 \cr
& y = {{{D_y}} \over D} = {{{{(m + 4)}^2}} \over { - (m + 4)}} = - m - 4 \cr} \)
+ Với \(m = -4\), hệ có vô số nghiệm với \((x; x – 3), x ∈ \mathbb R\)
