Bài 22. Cho tam giác \(OAB\). Gọi \(M, N\) lần lượt là trung điểm hai cạnh \(OA\) và \(OB\). Hãy tìm các số \(m\) và \(n\) thích hợp trong mỗi đẳng thức sau đây
\(\eqalign{
& \overrightarrow {OM} = m\overrightarrow {OA} + n\overrightarrow {OB} ;\,\,\,\,\,\,\overrightarrow {MN} = m\overrightarrow {OA} + n\overrightarrow {OB} ; \cr
& \overrightarrow {AN} = m\overrightarrow {OA} + n\overrightarrow {OB} ;\,\,\,\,\,\,\,\,\overrightarrow {MB} = m\overrightarrow {OA} + n\overrightarrow {OB} . \cr} \)

Advertisements (Quảng cáo)
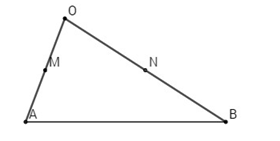
Ta có
\(\eqalign{
& \overrightarrow {OM} = {1 \over 2}\overrightarrow {OA} = {1 \over 2}\overrightarrow {OA} + 0.\overrightarrow {OB} \,\,\,\,\, \Rightarrow \,m = {1 \over 2},\,n = 0. \cr
& \overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} = {1 \over 2}\overrightarrow {OB} - {1 \over 2}\overrightarrow {OA} = \left( { - {1 \over 2}} \right)\overrightarrow {OA} + {1 \over 2}\overrightarrow {OB} \,\,\,\,\, \Rightarrow \,m = - {1 \over 2},\,n = {1 \over 2}. \cr
& \overrightarrow {AN} = \overrightarrow {ON} - \overrightarrow {OA} = {1 \over 2}\overrightarrow {OB} - \overrightarrow {OA} = \left( { - 1} \right)\overrightarrow {OA} + {1 \over 2}\overrightarrow {OB} \,\,\,\, \Rightarrow \,m = - 1,\,n = {1 \over 2}. \cr
& \overrightarrow {MB} = \overrightarrow {OB} - \overrightarrow {OM} = \overrightarrow {OB} - {1 \over 2}\overrightarrow {OA} = \left( { - {1 \over 2}} \right)\overrightarrow {OA} + \overrightarrow {OB} \,\,\,\, \Rightarrow \,m = - {1 \over 2},\,n = 1. \cr} \)
