Bài 28. Cho tứ giác \(ABCD\). Chứng minh rằng
a) Có một điểm \(G\) duy nhất sao cho \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Điểm \(G\) như thế gọi là trọng tâm của bốn điểm \(A, B, C, D\). Tuy nhiên, người ta vẫn quen gọi \(G\) là trọng tâm của từ giác \(ABCD\).
b) Trọng tâm \(G\) là trung điểm của mỗi đoạn thẳng nối các trung điểm hai cạnh đối của tứ giác, nó cũng là trung điểm của đoạn thẳng nối trung điểm hai đường chéo của tam giác.
c) Trọng tâm \(G\) nằm trên các đoạn thẳng nối một đỉnh của tứ giác và trọng tâm của tam giác tạo bởi ba đỉnh còn lại.

a) Gọi \(O\) là điểm cố định bất kì, ta có
\(\eqalign{
& \,\,\,\,\,\,\,\,\,\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \cr
& \Leftrightarrow \,\,\,\overrightarrow {OA} - \overrightarrow {OG} + \overrightarrow {OB} - \overrightarrow {OG} + \overrightarrow {OC} - \overrightarrow {OG} + \overrightarrow {OD} - \overrightarrow {OG} = \overrightarrow 0 \cr
& \Leftrightarrow \,\,\,4\overrightarrow {OG} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \cr
& \Leftrightarrow \,\,\,\overrightarrow {OG} = {1 \over 4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right). \cr} \)
Vậy \(G\) là điểm xác định duy nhất sao cho \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 .\)
b)
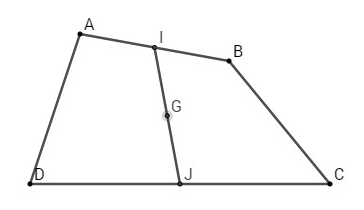
Gọi \(I, J\) lần lượt la trung điểm của \(AB, CD\) ta có
Advertisements (Quảng cáo)
\(\eqalign{
& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \, \cr
& \, \Rightarrow \,\,2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \,\, \Rightarrow \,\overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \, \cr} \)
\( \Rightarrow \,\,G\) là trung điểm \(IJ\)
Tương tự, ta gọi \(H, K\) lần lượt là trung điểm của \(AC, BD\) ta có
\(\eqalign{
& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \, \cr
& \, \Rightarrow \,\,2\overrightarrow {GH} + 2\overrightarrow {GK} = \overrightarrow 0 \,\, \Rightarrow \,\overrightarrow {GH} + \overrightarrow {GK} = \overrightarrow 0 \, \cr} \)
\( \Rightarrow \,\,G\) là trung điểm \(HK\)
Tương tự, ta cũng chứng minh được \(G\) là trung điểm của đoạn thẳng nối trung điểm hai đường chéo của tam giác.
c)
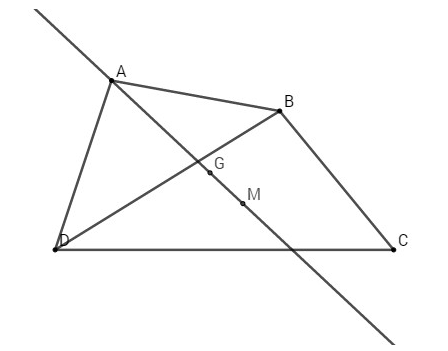
Gọi \(M\) là trọng tâm của tam giác \(BCD\), ta có
\(\eqalign{
& 3\overrightarrow {GM} = \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \,\,\, \Rightarrow \,3\overrightarrow {GM} + \overrightarrow {GA} = \overrightarrow 0 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \,\overrightarrow {GA} = - 3\overrightarrow {GM} \,\,\,\,\,\,\,\,\,\,\,\,\,\, \cr} \)
Do đó, \(G, A, M\) thẳng hàng.
Các trường hợp còn lại làm tương tự.Vậy trọng tâm \(G\) nằm trên các đoạn thẳng nối một đỉnh của tứ giác và trọng tâm của tam giác tạo bởi ba đỉnh còn lại.
