Advertisements (Quảng cáo)
Bài 21. Cho tam giác vuông cân \(OAB\) với \(OA = OB = a\). Hãy dựng các vec tơ sau đây và tính độ dài của chúng
\(\eqalign{
& \overrightarrow {OA} + \overrightarrow {OB} ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\;\overrightarrow {OA} – \overrightarrow {OB} ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\overrightarrow {OA} + 4\overrightarrow {OB} ; \cr
& {{21} \over 4}\overrightarrow {OA} + 2,5\overrightarrow {OB} ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{11} \over 4}\overrightarrow {OA} – {3 \over 7}\overrightarrow {OB} . \cr} \)
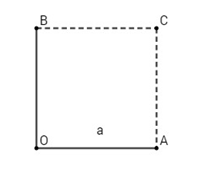
Vẽ hình vuông \(OACB\), ta có
\(\eqalign{
& \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \, \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right| = a\sqrt 2 \cr
& \overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {BA} \, \Rightarrow \left| {\overrightarrow {OA} – \overrightarrow {OB} } \right| = \left| {\overrightarrow {BA} } \right| = a\sqrt 2 \cr} \)
Gọi \(M, N\) là điểm thỏa mãn \(\overrightarrow {OM} = 3\overrightarrow {OA} ,\,\overrightarrow {ON} = 4\overrightarrow {OB} \).
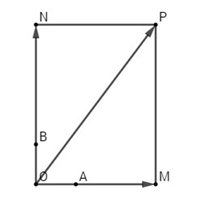
Vẽ hình chữ nhật \(MONP\), ta có
\(\eqalign{
& \overrightarrow {OM} + \overrightarrow {ON} = \overrightarrow {OP} \, \Rightarrow \left| {\overrightarrow {OM} + \overrightarrow {ON} } \right| = \left| {\overrightarrow {OP} } \right| \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {O{M^2} + O{N^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {9{a^2} + 16{a^2}} = 5a \cr
& \cr} \)
Advertisements (Quảng cáo)
Tương tự, ta cũng có
\(\eqalign{
& \left| {{{21} \over 4}\overrightarrow {OA} + 2,5\overrightarrow {OB} } \right| = \sqrt {{{\left( {{{21} \over 4}a} \right)}^2} + {{\left( {{5 \over 2}a} \right)}^2}} = {{\sqrt {541} } \over 4}a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cr} \)
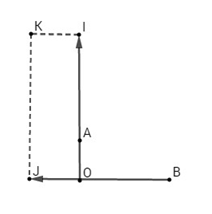
Gọi \(I, J\) là điểm thỏa mãn
\(\overrightarrow {OI} = {{11} \over 4}\overrightarrow {OA} ,\,\overrightarrow {OJ} = – {3 \over 7}\overrightarrow {OB} \)
Vẽ hình chữ nhật \(OIKJ\), ta có
\(\eqalign{
& {{11} \over 4}\overrightarrow {OA} – {3 \over 7}\overrightarrow {OB} = \overrightarrow {OK} = {{11} \over 4}\overrightarrow {OA} + \left( { – {3 \over 7}\overrightarrow {OB} } \right) = \overrightarrow {OI} + \overrightarrow {OJ} = \overrightarrow {OK} \cr
& \Rightarrow \,\left| {{{11} \over 4}\overrightarrow {OA} – {3 \over 7}\overrightarrow {OB} } \right| = \left| {\overrightarrow {OK} } \right| = \sqrt {{{\left( {{{11} \over 4}a} \right)}^2} + {{\left( { – {3 \over 7}a} \right)}^2}} = {{\sqrt {6073} } \over {28}}a \cr} \)