Bài 1. Xét dấu các biểu thức:
a) \(f(x) = (2x - 1)(x + 3)\);
b) \(f(x) = (- 3x - 3)(x + 2)(x + 3)\);
c)\( f(x) = \frac{-4}{3x+1}-\frac{3}{2-x};\)
d) \(f(x) = 4x^2– 1\).

a) Ta lập bảng xét dấu
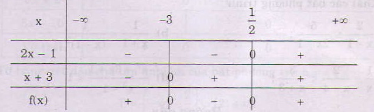
Kết luận: \(f(x) < 0\) nếu \(- 3 < x < \frac{1}{2}\)
\(f(x) = 0\) nếu \(x = - 3\) hoặc \(x = \frac{1}{2}\)
\(f(x) > 0\) nếu \(x < - 3\) hoặc \(x > \frac{1}{2}\).
b) Ta lập bảng xét dấu

\( f(x) < 0\) nếu \(x ∈ (- 3; - 2) ∪ (- 1; +∞)\)
\(f(x) = 0\) với \(x = - 3\), \(x= - 2\), hoặc \(x= - 1\)
Advertisements (Quảng cáo)
\( f(x) > 0\) với \(x ∈ (-∞; - 3) ∪ (- 2; - 1)\).
c) Ta có: \(f(x) = \frac{-4}{3x+1}-\frac{3}{2-x}=\frac{5x+11}{(3x+1)(x-2)}\)
Ta lập bảng xét dấu
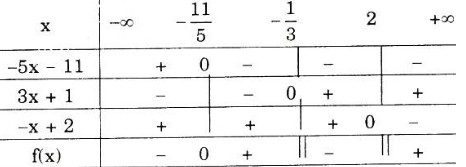
\(f(x)\) không xác định nếu \(x = -\frac{1}{3}\) hoặc \(x = 2\)
\(f(x) < 0\) với \(x ∈ \left ( -\infty ;-\frac{11}{5} \right )\) ∪ \(\left ( -\frac{1}{3};2 \right )\)
\(f(x) > 0\) với \(x ∈ \left ( -\frac{11}{5};-\frac{1}{3} \right )∪ (2; +∞)\).
d) \(f(x) = 4x^2– 1 = (2x - 1)(2x + 1)\).
Ta lập bảng xét dấu
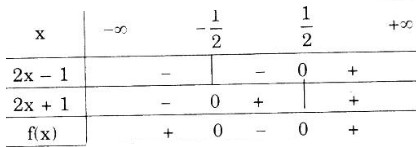
\(f(x) = 0\) với \(x = \pm \frac{1}{2}\)
\(f(x) < 0\) với \(x ∈ \left ( -\frac{1}{2};\frac{1}{2} \right )\)
\(f(x) > 0\) với \(x ∈ \left ( -\infty ;-\frac{1}{2} \right )∪ \left ( \frac{1}{2};+\infty \right ).\)
