Định nghĩa : Trong mặt phẳng, cho hai điểm cố định \(F_1\) và \(F_2\)
Elip là tập hợp các điểm \(M\) sao cho tổng \(F_1M +F_2M = 2a\) không đổi
Các điểm \(F_1\) và \(F_2\) gọi là tiêu điểm của elip
Khoảng cách \(F_1.F_2= 2c\) gọi là tiêu cự của elip
2. Phương trình chính tắc của elip
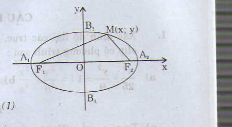
Cho elip có tiêu điểm \(F_1\) và \(F_2\) chọn hệ trục tọa độ \(Oxy\) sao cho \(F_1(-c ; 0)\) và \(F_2(c ; 0)\). Khi đó người ta chứng minh được
\(M(x ; y) \in\) elip \(\Rightarrow\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}} = 1\) (1)
trong đó: \(b^2= a^2– c^2\)
Phương trình (1) gọi là phương trình chính tắc của elip
Advertisements (Quảng cáo)
3. Hình dạng của elip
Xét elip \((E)\) có phương trình (1):
a) Nếu điểm \(M(x; y)\) thuộc \((E)\) thì các điểm \(M_1(-x ; y) M_2(x ;- y)\) và \(M_3(-x ; -y)\) cũng thuộc \((E)\).
Vậy \((E)\) có các trục đối xứng là \(Ox, Oy\) và có tâm đối xứng là gốc \(O\).
b) Thay \(y = 0\) vào (1) ta có \(x = ±a\) suy ra \((E)\) cắt \(Ox\) tại hai điểm \(A_1(-a ; 0) A_2(a ;0)\).
Tương tự thay \(x = 0\) vào (1) ta được \(y = ±b\), vậy \((E)\) cắt \(Oy\) tại hai điểm \( B_1(0 ; -b) B_2(0 ;b)\).
Các điểm \(A_1, A_2, B_1, B_2\) gọi là các đỉnh của elip
Đoạn thẳng \(A_1A_2\) gọi là trục lớn, đoạn thẳng \(B_1,B_2\) gọi là trục nhỏ của elip