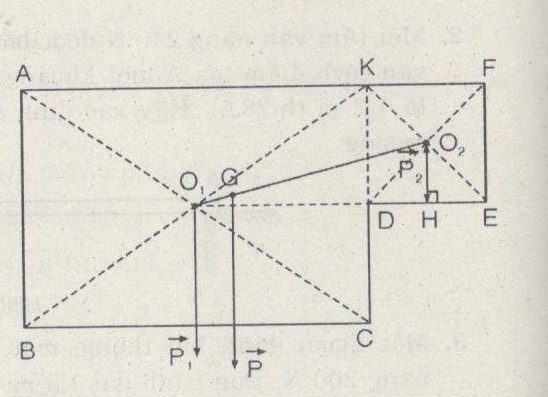
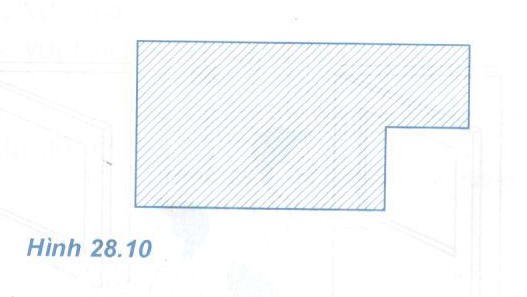
Hãy xác định trọng tâm của một bản mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một mẩu hình vuông có cạnh 3 cm (Hình 28.10).

Advertisements (Quảng cáo)
Hình dung hình phẳng (cần phải xác định trọng tâm G) được ghép từ hai hình phẳng: Hình chữ nhật ABCK và hình vuông DEFK với \(\eqalign{ & {S_{ABCK}} = 6.{S_{{\rm{DEFK}}}} \cr & = > {P_{ABCK}} = 6{P_{{\rm{DEFK}}}}\,hay\,{P_1} = 6{P_2} \cr & < = > {{{P_1}} \over {{P_2}}} = 6 \cr & {O_2}H = 1,5cm;{O_1}H = 4,5 + 1,5 = 6(cm) \cr & {O_1}{O_2} = \sqrt {{O_2}{H^2} + {O_1}{H^2}} \cr&\;\;\;\;\;\;\;\;\;\;= \sqrt {1,{5^2} + {6^2}} = 6,18(cm) \cr} \)
Trọng lực \(\overrightarrow P \,\) của hình phẳng sẽ là hợp lực của hai lực song song cùng chiều: \(\overrightarrow P = \overrightarrow {{P_1}} + \overrightarrow {{P_2}} \,\) nên trọng tâm G của hình nằm trên đoạn O1O2 sao cho: \(\eqalign{ & {{G{O_2}} \over {G{O_1}}} = {{{P_1}} \over {{P_2}}} = 6 = > {{G{O_2} + G{O_1}} \over {G{O_1}}} = 6 + 1 \cr & < = > {{{O_1}{O_2}} \over {G{O_1}}} = 7 \cr&= > G{O_1} = {{{O_1}{O_2}} \over 7} = {{6,18} \over 7} = 0,88(cm) \cr} \)