Một con lắc đơn có chiều dài l=1m. Kéo cho dây làm với phương thẳng đứng góc \(\alpha = {45^0}\) rồi thả tự do.Tìm vận tốc của con lắc khi nó đi qua:
a) vị trí ứng với góc 300;
b) vị trí cân bằng.

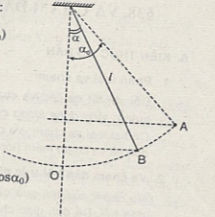
Chọn \({{\rm{W}}_{{t_0}}} = 0\) thì cơ năng tại \(A({\alpha _0})\) là :
\({\rm{W}} = {{\rm{W}}_{{t_A}}} = mg{z_A} = mg(l - l\cos {\alpha _0})\)
Advertisements (Quảng cáo)
Thế năng tại \(B(\alpha ):{{\rm{W}}_t} = mgl(1 - \cos \alpha )\)
Động năng tại B: \({{\rm{W}}_đ} = {{m{v^2}} \over 2}\)
Áp dụng định luật bảo toàn cơ năng:
\(\eqalign{ & {{\rm{W}}_B} = {{\rm{W}}_A} \Leftrightarrow {{\rm{W}}_t} + {{\rm{W}}_đ} = {\rm{W}} \cr & \Leftrightarrow mgl(l - \cos \alpha ) + {{m{v^2}} \over 2} = mgl(1 - \cos {\alpha _0}) \cr & v = \sqrt {2gl(cos\alpha - \cos {\alpha _0})} \cr} \)
\(\eqalign{ & a)\alpha = {30^0} \Rightarrow v = \sqrt {2.9,8.1\left( {{{\sqrt 3 } \over 2} - {{\sqrt 2 } \over 2}} \right)} \cr& \approx 1,76(m/s) \cr & b)\alpha = {0^0} \Rightarrow v = \sqrt {2.9,8.2\left( {1 - {{\sqrt 2 } \over 2}} \right)} \cr& \approx 2,40(m/s) \cr} \)
