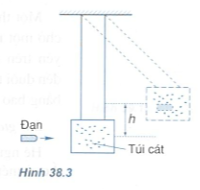
Bắn một viên đạn khối lượng m=10g với vận tốc v vào một túi cát treo nằm trên có khối lượng M=1kg. Va chạm là mềm, đạn mắc lại trong túi cát và chuyển động cùng với túi cát.
a) Sau va chạm, túi cát được nâng lên độ cao h=0,8m so với vị trí cân bằng ban đầu( Hình 38.3). Hãy tìm vận tốc của đạn (túi cát được gọi là con lắc thử đạn vì nó cho phép xác định vận tốc của đạn ).
b) Bao nhiêu phần trăm động năng ban đầu đã chuyển thành nhiệt lượng và các dạng năng lượng khác ?

Bỏ qua lực cản không khí.
Áp dụng định luật bảo toàn động lượng cho quá trình đạn va chạm với bao cát.
Advertisements (Quảng cáo)
\(mv = \left( {M + m} \right)V \Rightarrow v = {{M + m} \over m}V\;\;\;(1)\)
Áp dụng định luật bảo toàn cơ năng cho quá trình đi lên cao của “ bao cát +đạn”
Với mức không thế năng ở vị trí thấp nhất :
\({{\left( {M + m} \right){V^2}} \over 2} = (M + m)gh \Rightarrow V = \sqrt {2gh}\;\;\; (2)\)
Thay (2) và (1) được vận tốc đạn trước khi vào cát là
\(\eqalign{ & v = {{M + m} \over m}\sqrt {2gh} = {{1,01} \over {0,01}}\sqrt {2.9,8.0,8} \approx 400m/s \cr & {{\left| {\Delta {{\rm{W}}_đ}} \right|} \over {{{\rm{W}}_đ}}} = {{{{\rm{W}}_đ} - {\rm{W}}_đ’} \over {{{\rm{W}}_đ}}} = 1 - {{\left( {M + m} \right)gh} \over {{m \over 2}{{\left( {{{M + m} \over m}} \right)}^2}.2gh}} \cr & = 1 - {m \over {M + m}} = {M \over {m + M}} = {1 \over {1,01}} \approx 0,99 \cr & {{\left| {\Delta {{\rm{W}}_đ}} \right|} \over {{{\rm{W}}_đ}}} = 99\% \cr} \)
