
Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\), \(AD\). Giao tuyến của hai mặt phẳng \(\left( {CMN} \right)\) và \(\left( {BCD} \right)\) là đường thẳng song song với đường thẳng nào sau đây?
A. \(BD\)
B. \(CD\)
C. \(BC\)
D. \(AB\)

Chứng minh rằng \(MN\parallel BD\).
Advertisements (Quảng cáo)
Sử dụng tính chất sau: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó, hoặc trùng với một trong hai đường thẳng đó.

Ta có \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AD\), nên \(MN\) là đường trung bình của tam giác \(ABD\). Suy ra \(MN\parallel BD\).
Xét hai mặt phẳng \(\left( {CMN} \right)\) và \(\left( {BCD} \right)\). Ta có \(C \in \left( {CMN} \right) \cap \left( {BCD} \right)\) nên tồn tại giao tuyến giữa hai mặt phẳng \(\left( {CMN} \right)\) và \(\left( {BCD} \right)\). Hơn nữa, do \(C \notin BD\) nên \(BD\) không là giao tuyến của hai mặt phẳng trên.
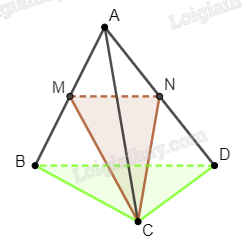
Ta thấy rằng, \(MN\parallel BD\), \(MN \subset \left( {CMN} \right)\), \(BD \subset \left( {BCD} \right)\), nên suy ra giao tuyến của hai mặt phẳng \(\left( {CMN} \right)\) và \(\left( {BCD} \right)\) song song hoặc trùng với \(BD\).
Nhưng do \(BD\) không là giao tuyến của hai mặt phẳng \(\left( {CMN} \right)\) và \(\left( {BCD} \right)\), nên giao tuyến của chúng song song với đường thẳng \(BD\).
Đáp án đúng là A.
