
Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình thang với đáy lớn \(AD\). Gọi \(M\) là trọng tâm của tam giác \(SAD\), \(N\) là điểm thuộc đoạn thẳng \(AC\) sao cho \(AN = \frac{1}{3}AC\), \(P\) là điểm thuộc đoạn thẳng \(CD\) sao cho \(DP = \frac{1}{3}DC\). Chứng mình rằng \(\left( {MNP} \right)\parallel \left( {SBC} \right)\).

Sử dụng định lý Thales, do \(\frac{{AN}}{{AC}} = \frac{{DP}}{{DC}}\) nên \(NP\parallel AD\), suy ra \(NP\parallel BC\) và \(NP\parallel \left( {SBC} \right)\). Gọi \(I\) là giao điểm của \(NP\) và \(EC\). Áp dụng định lý Thales ta suy ra \(\frac{{EI}}{{EC}} = \frac{1}{3}\), từ đó chứng minh được \(IM\parallel SC\) và \(IM\parallel \left( {SBC} \right)\), rồi suy ra điều phải chứng minh.

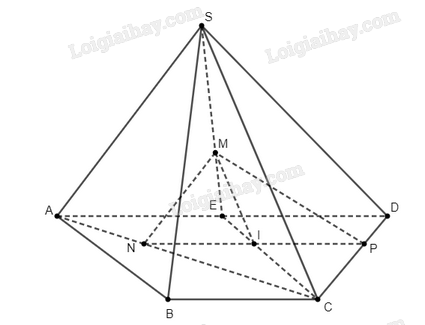
Ta có \(\frac{{AN}}{{AC}} = \frac{{DP}}{{DC}}\left( { = \frac{1}{3}} \right)\) nên theo định lý Thales, ta có \(NP\parallel AD\).
Do \(ABCD\) là hình thang với đáy lớn \(AD\), ta có \(AD\parallel BC\). Như vậy \(NP\parallel BC\).
Advertisements (Quảng cáo)
Mà \(BC \subset \left( {SBC} \right)\), ta kết luận rằng \(NP\parallel \left( {SBC} \right)\).
Gọi \(E\) là trung điểm của \(AD\).
Do \(M\) là trọng tâm của tam giác \(SAD\) nên \(M \in SE\) và \(\frac{{SM}}{{SE}} = \frac{2}{3}\). Từ đó\(\frac{{EM}}{{ES}} = \frac{1}{3}\).
Gọi \(I\) là giao điểm của \(NP\) và \(EC\).
Xét tam giác \(CDE\), ta có \(IP\parallel DE \Rightarrow \frac{{EI}}{{EC}} = \frac{{DP}}{{DC}} = \frac{1}{3}\).
Vậy \(\frac{{EI}}{{EC}} = \frac{{EM}}{{ES}}\left( { = \frac{1}{3}} \right)\), từ đó ta có \(MI\parallel SC\). Do \(SC \subset \left( {SBC} \right)\) nên \(MI\parallel \left( {SBC} \right)\).
Như vậy ta có \(NP\parallel \left( {SBC} \right)\), \(MI\parallel \left( {SBC} \right)\). Mà \(NP \cap MI = \left\{ I \right\}\), nên ta suy ra \(\left( {MNP} \right)\parallel \left( {SBC} \right)\).
Bài toán được chứng minh.
