
Cho hình hộp \(ABCD.A’B’C’D’\). Khẳng định nào sau đây là SAI?
A. Các mặt của hình hộp là các hình bình hành.
B. Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.
C. Các đoạn thẳng \(AC’\), \(A’C\), \(BD’\), \(B’D\) bằng nhau.
D. Các đường thẳng \(AC’\), \(A’C\), \(BD’\), \(B’D\) đồng quy.

Sử dụng định nghĩa và các tính chất của hình hộp.
Advertisements (Quảng cáo)

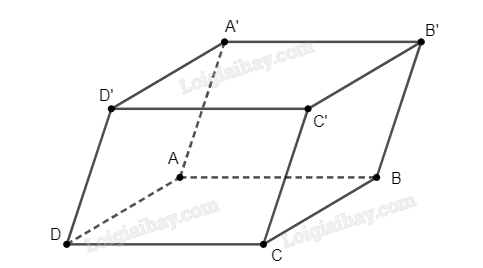
Đáp án A đúng vì hình hộp là hình lăng trụ có đáy là hình bình hành, mà các mặt bên của lăng trụ cũng là hình bình hành.
Đáp án B đúng vì theo tính chất của hình hộp, hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.
Đáp án C sai, vì \(DBB’D’\) là hình bình hành, nên không đủ kết luận để chỉ ra rằng \(DB’ = D’B\).
Đáp án D đúng, vì các tứ giác \(DBB’D’\), \(ACC’A’\), \(ABC’D’\) là các hình bình hành, nên 4 đường thẳng \(AC’\), \(A’C\), \(BD’\), \(B’D\) cắt nhau tại trung điểm của mỗi đường.
Đáp án cần chọn là đáp án C.
