
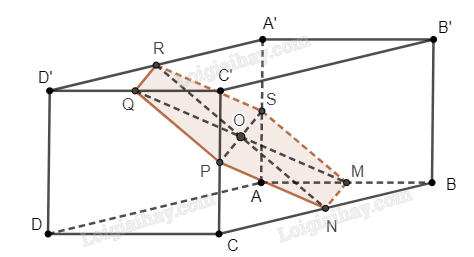
Cho hình hộp \(ABCD.A’B’C’D’\). Gọi \(M\), \(N\), \(P\), \(Q\), \(R\), \(S\) lần lượt là trung điểm của \(AB\), \(BC\), \(CC’\), \(C’D’\), \(D’A’\), \(AA’\). Chứng minh rằng:
a) Sáu điểm \(M\), \(N\), \(P\), \(Q\), \(R\), \(S\) cùng thuộc một mặt phẳng.
b) Các đoạn thẳng \(MQ\), \(NR\), \(PS\) cắt nhau tại trung điểm của mỗi đoạn.

a) Chỉ ra rằng \(RS\parallel NP\), \(PQ\parallel MS\) và \(QR\parallel MN\) để chỉ ra 6 điểm đồng phẳng.
b) Chứng minh rằng \(MNQR\), \(RSNP\) là các hình bình hành để suy ra điều phải chứng minh.

Advertisements (Quảng cáo)
a) Do \(R\) là trung điểm \(A’D’\), \(S\) là trung điểm \(AA’\) nên \(RS\) là đường trung bình của tam giác \(A’AD’\). Suy ra \(RS\parallel AD’\). Tương tự ta cũng có \(NP\parallel BC’\).
Tứ giác \(ABC’D’\) có \(AB = C’D’\) và \(AB\parallel C’D’\) nên là hình bình hành. Suy ra \(AD’\parallel BC’\) và \(AD’ = BC’\). Từ đó suy ra \(RS\parallel NP\), và 4 điểm \(R\), \(S\), \(N\), \(P\) đồng phẳng.
Chứng minh tương tự ta có \(PQ\parallel MS\) và \(QR\parallel MN\).
Như vậy, 6 điểm \(M\), \(N\), \(P\), \(Q\), \(R\), \(S\) đồng phẳng. Bài toán được chứng minh.
b) Ta có \(RS\parallel NP\).
Vì \(RS\) là đường trung bình của tam giác \(A’AD’\) nên \(RS = \frac{1}{2}AD’\). Tương tự ta cũng có \(NP = \frac{1}{2}BC’\). Do \(AD’ = BC’\) nên \(RS = NP\). Vậy tứ giác \(RSNP\) là hình bình hành. Suy ra \(NR\) và \(PS\) cắt nhau tại trung điểm \(O\) của mỗi đường.
Chứng minh tương tự ta cũng có \(MNQR\) là hình bình hành, từ đó ta có \(NR\) và \(MQ\) cắt nhau tại trung điểm của mỗi đường. Do \(O\) là trung điểm của \(NR\), nên \(O\) cũng là trung điểm của \(MQ\).
Vậy ba đoạn thẳng \(MQ\), \(NR\) và \(PS\) cắt nhau trung điểm \(O\) của mỗi đường.
Bài toán được chứng minh.
