
Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh \(a\sqrt 2 \). Biết rằng \(SA = SB = SC = SD,SO = 2a\sqrt 2 \).
a) Chứng minh rằng \(SO \bot \left( {ABCD} \right)\).
b) Tính độ dài đường cao xuất phát từ đỉnh A của tam giác SAC.

Sử dụng kiến thức về định lý đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).

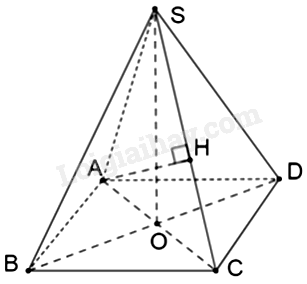
a) Vì ABCD là hình vuông tâm O nên O là trung điểm của AC, O là trung điểm của BD.
Vì \(SA = SC\) nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác SAC. Do đó, \(SO \bot AC\)
Vì \(SB = SD\) nên tam giác SBD cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác SBD. Do đó, \(SO \bot BD\)
Advertisements (Quảng cáo)
Vì \(SO \bot AC\), \(SO \bot BD\), AC và BD cắt nhau và nằm trong mặt phẳng (ABCD).
Do đó, \(SO \bot \left( {ABCD} \right)\)
b) Kẻ \(AH \bot SC\left( {H \in SC} \right)\)
Áp dụng định lý Pythagore vào tam giác ABC vuông tại B có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = 2a\)
Suy ra: \(OC = \frac{{AC}}{2} = a\)
Vì \(SO \bot \left( {ABCD} \right),OC \subset \left( {ABCD} \right) \Rightarrow SO \bot OC\)
Áp dụng định lý Pythagore vào tam giác SOC vuông tại O có:
\(SC = \sqrt {O{C^2} + S{O^2}} = \sqrt {{a^2} + {{\left( {2a\sqrt 2 } \right)}^2}} = 3a\)
Ta có: \(AH.SC = SO.AC\left( { = 2{S_{\Delta SAC}}} \right) \Rightarrow AH = \frac{{SO.AC}}{{SC}} = \frac{{2a\sqrt 2 .2a}}{{3a}} = \frac{{4a\sqrt 2 }}{3}\)
