
Cho tứ diện ABCD có \(AB \bot CD\) và \(AC \bot BD\). Gọi H là hình chiếu vuông góc của A xuống mặt phẳng (BCD). Chứng minh rằng H là trực tâm của \(\Delta \)BCD. Và \(AD \bot BC\)

Sử dụng kiến thức về định lý đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).

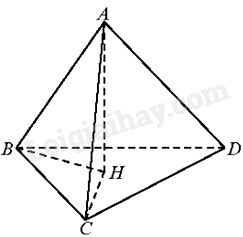
Vì H là hình chiếu vuông góc của A xuống mặt phẳng (BCD) nên \(AH \bot \left( {BCD} \right)\)
Advertisements (Quảng cáo)
Mà \(CD,BD,BC \subset \left( {BCD} \right) \Rightarrow AH \bot CD,AH \bot BD,AH \bot BC\)
Vì \(AH \bot CD\), \(AB \bot CD\) nên \(CD \bot \left( {ABH} \right) \Rightarrow CD \bot BH\)
Vì \(AH \bot BD\), \(AC \bot BD\) nên \(BD \bot \left( {AHC} \right) \Rightarrow BD \bot HC\)
\(\Delta \)BCD có hai đường cao BH và CH cắt nhau tại H nên H là trực tâm của \(\Delta \)BCD.
Do đó, \(BC \bot DH\)
Lại có: \(AH \bot BC\) nên \(BC \bot \left( {ADH} \right)\). Mà \(AD \subset \left( {ADH} \right)\) nên \(BC \bot AD\)
