
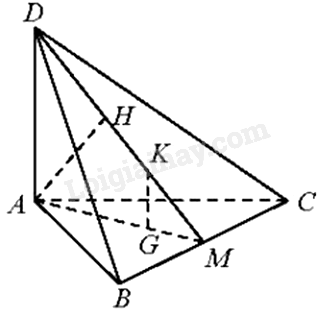
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ \(AH \bot MD\) tại H.
a) Chứng minh rằng \(AH \bot \left( {BCD} \right)\).
b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng \(GK \bot \left( {ABC} \right)\).

a) Sử dụng kiến thức về định lý đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
b) Sử dụng kiến thức về liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng: Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

Advertisements (Quảng cáo)
a) Vì \(DA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow DA \bot BC\)
Tam giác ABC cân tại A nên AM là đường trung tuyến đồng thời là đường cao, suy ra: \(BC \bot AM\)
Vì \(DA \bot BC\), \(BC \bot AM\), DA và AM cắt nhau tại A và nằm trong (DAM) nên \(BC \bot \left( {DAM} \right)\). Lại có, \(AH \subset \left( {DAM} \right) \Rightarrow AH \bot BC\)
Ta có: \(AH \bot MD\), \(AH \bot BC\), MD và BC cắt nhau tại M và nằm trong (BCD) nên \(AH \bot \left( {BCD} \right)\)
b) Tam giác DBC có K là trọng tâm và DM là đường trung tuyến nên \(\frac{{DK}}{{DM}} = \frac{2}{3}\)
Tam giác ABC có G là trọng tâm và AM là đường trung tuyến nên \(\frac{{AG}}{{AM}} = \frac{2}{3}\)
Tam giác ADM có: \(\frac{{DK}}{{DM}} = \frac{{AG}}{{AM}}\left( { = \frac{2}{3}} \right)\) nên KG//AD (định lý Thalès đảo)
Mà \(DA \bot \left( {ABC} \right)\) nên \(GK \bot \left( {ABC} \right)\).
