
Cho hình lăng trụ đều ABC. A’B’C’ có cạnh đáy bằng a. Biết \(d\left( {A,\left( {A’BC} \right)} \right) = \frac{{a\sqrt {57} }}{{12}}\). Tính \({V_{ABC.A’B’C’}}\).

+ Sử dụng kiến thức về khoảng cách từ điểm đến mặt phẳng để tính: Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn thẳng MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M; (P)).
+ Sử dụng kiến thức về thể tích khối lăng trụ: Thể tích khối lăng trụ bằng diện tích đáy nhân với chiều cao: \(V = S.h\)

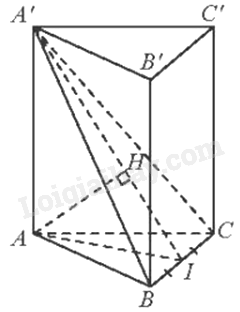
Vì ABC. A’B’C’ là lăng trụ đều \(A’A \bot \left( {ABC} \right) \Rightarrow A’A \bot BC\)
Gọi I là trung điểm của BC. Tam giác ABC đều nên AI là đường trung tuyến đồng thời là đường cao. Do đó, \(AI \bot BC\)
Advertisements (Quảng cáo)
Ta có: \(A’A \bot BC\), \(AI \bot BC\) nên \(BC \bot \left( {A’AI} \right)\)
Trong mặt phẳng (A’AI), kẻ \(AH \bot A’I\left( {H \in A’I} \right) \Rightarrow BC \bot AH\)
Vì \(BC \bot AH,AH \bot A’I\) nên \(AH \bot \left( {A’BC} \right)\). Do đó, \(d\left( {A,\left( {A’BC} \right)} \right) = AH = \frac{{a\sqrt {57} }}{{12}}\).
Tam giác ABC đều nên AI là đường trung tuyến đồng thời là đường cao. Do đó, tam giác ABI vuông tại I. Suy ra: \(AI = AB.\sin \widehat {ABC} = \frac{{a\sqrt 3 }}{2}\)
Vì \(A’A \bot \left( {ABC} \right) \Rightarrow A’A \bot AI\)
Tam giác A’AI vuông tại A, AH là đường cao có:
\(\frac{1}{{A'{A^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{I^2}}} = \frac{{144}}{{57{a^2}}} - \frac{4}{{3{a^2}}} = \frac{{68}}{{57{a^2}}} \\ \Rightarrow A’A = \frac{{a\sqrt {969} }}{{34}}\)
Thể tích lăng trụ ABC. A’B’C’ là: \({V_{ABC.A’B’C’}} = A’A.{S_{ABC}} = A’A.\frac{1}{2}.AI.BC \\ = \frac{1}{2}\frac{{a\sqrt {969} }}{{34}}.\frac{{a\sqrt 3 }}{2}.a = \frac{{3{a^3}\sqrt {323} }}{{136}}\)
