Từ \(O\) dựng các đường thẳng \(d’_1, d’_2\) lần lượt song song có thể trùng nếu \(O\) nằm trên một trong hai đường thẳngvới \({d_1}\) và \({d_2}\). Gợi ý giải - Bài 7.2 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống - Bài 22. Hai đường thẳng vuông góc. Cho hình hộp có tất cả các cạnh bằng nhau và góc bằng...

Cho hình hộp có tất cả các cạnh bằng nhau và góc A’AD bằng . Tính góc giữa các cặp đường thẳng sau: A’C và BD AD và BB’;A’D và BB’.

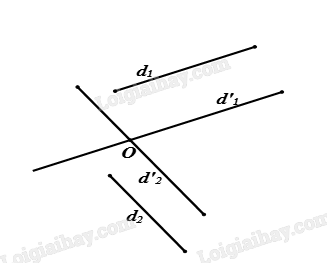
Từ \(O\) dựng các đường thẳng \(d’_1,d’_2\) lần lượt song song có thể trùng nếu \(O\) nằm trên một trong hai đường thẳngvới \({d_1}\) và \({d_2}\). Góc giữa hai đường thẳng \(d’_1,d’_2\)chính là góc giữa hai đường thẳng\({d_1},{d_2}\).
Lưu ý : Hai đường chéo của hình thoi hoặc hình vuông thì vuông gói với nhau
Advertisements (Quảng cáo)

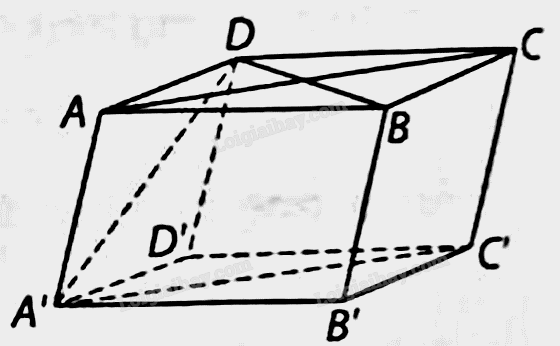
Vì ABCD là hình thoi và A’C’//AC nên (A’C’,BD)=(AC,BD)=90O
Vì BB’//AA’ nên (AD,BB’) = (AD,AA’) = 180O - \(\widehat {AA’D}\) = 60O \) và
\(\left( {A’D,BB’} \right) = \left( {A’D,AA’} \right) = \widehat {AA’D} = {30^ \circ }\)
