
Cho hình chóp tứ giác đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), cạnh bên \(SA = \frac{{a\sqrt 5 }}{2}\). Gọi \(SM,SN\) lần lượt là đường cao của tam giác \(SAD\) và tam giác \(SBC\).
a) Chứng minh rằng \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).
b) Tính số đo của góc nhị diện \([S,AD,B]\).
Xác định
c) Tính theo a thể tích khối chóp \(S.ABCD\).

a) Chứng minh rằng \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).
Chứng minh mặt phẳng \(\left( {ABCD} \right)\) chứa \(BC \bot \) \(\left( {SMN} \right).\)
b) Tính số đo của góc nhị diện \([S,AD,B]\).
- Xác định được \(\left[ {S,AD,B} \right] = \widehat {SMO}\)
- Tính \(\widehat {SMO}\)
Advertisements (Quảng cáo)
c) Tính theo a thể tích khối chóp \(S.ABCD\).
- Gọi \(O = AC \cap BD\)
- Tính chiều cao \(SO,{S_{ABCD}}\)
- Tính thể tích khối chóp \(S.ABCD = \frac{1}{3}SO.{S_{ABCD}}\).

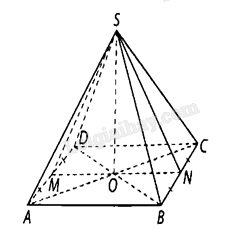
a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Ta có: \(AD \bot SM,AD//BC\) nên \(BC \bot SM\), mà \(BC \bot SN\), suy ra \(BC \bot \left( {SMN} \right).\)
Do đó \(\left( {SMN} \right) \bot \left( {ABCD} \right)\).
b) Vì \(MN\) đi qua \(O\) và \(OM \bot AD,SM \bot AD\) nên \(\left[ {S,AD,B} \right] = \widehat {SMO}\), ta tính được\(SM = SN = MN = a\). Do đó tam giác \(SMN\) đều, suy ra \(\widehat {SMN} = {60^ \circ }\).
Vậy \(\left[ {S,AD,B} \right] = {60^ \circ }\).
c) Ta có: \(SO = \frac{{a\sqrt 3 }}{2},{S_{ABCD}} = {a^2}\), suy ra \({V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{{{a^3}\sqrt 3 }}{6}\).
