
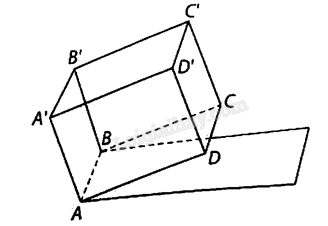
Một bể chứa nước hình hộp chữ nhật \(ABCD \cdot A’B’C’D’\) được đặt trên một mái nhà nghiêng so với mặt đất nằm ngang góc \({10^ \circ },AB = 1{\rm{\;m}},AD = 1,5{\rm{\;m}}\), \(AA’ = 1{\rm{\;m}}\). Đáy bể là hình chữ nhật \(ABCD\). Các điểm \(A,B\) cùng ở độ cao \(5{\rm{\;m}}\) (so với mặt đất), các điểm \(C,D\) ở độ cao lớn hơn so với độ cao của các điểm \(A,B\). Khi nước trong bể phẳng lặng người ta đo được khoảng cách giữa đường mép nước ở mặt phẳng \(\left( {ABB’A’} \right)\) và mặt đáy của bể là \(80{\rm{\;cm}}\). Tính thế tích của phần nước trong bể.

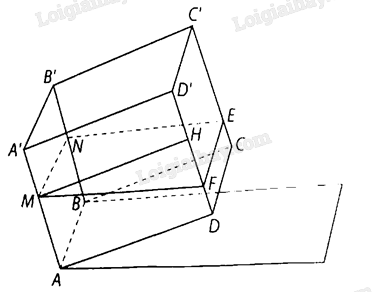
Gọi \(MN\) là đường mép nước ở trên mặt \(\left( {ABB’A’} \right),EF\) là đường mép nước trên mặt \(\left( {CDD’C’} \right)\).
Khi đó \(ABNM.DCEF\) là một hình chóp cựt.
Kẻ \(MH\) vuông góc với \(DD’\) tại \(H\) thì \(HF = MH \cdot {\rm{tan}}{10^ \circ } = {\rm{tan}}{10^ \circ }\left( {\rm{m}} \right)\).
Suy ra \(DF = DH - HF = AM - HF = 0,8 - {\rm{tan}}{10^ \circ } \approx 0,62\left( {{\rm{\;m}}} \right)\).
Tính: \({S_1} = {S_{DCEF}};{S_2} = {S_{ABNM}}\).
Advertisements (Quảng cáo)
Tính \(V = \frac{1}{3} \cdot \left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right) \cdot AD\)


Gọi \(MN\) là đường mép nước ở trên mặt \(\left( {ABB’A’} \right),EF\) là đường mép nước trên mặt \(\left( {CDD’C’} \right)\).
Khi đó \(ABNM.DCEF\) là một hình chóp cựt.
Kẻ \(MH\) vuông góc với \(DD’\) tại \(H\) thì \(HF = MH \cdot {\rm{tan}}{10^ \circ } = {\rm{tan}}{10^ \circ }\left( {\rm{m}} \right)\).
Suy ra \(DF = DH - HF = AM - HF = 0,8 - {\rm{tan}}{10^ \circ } \approx 0,62\left( {{\rm{\;m}}} \right)\).
Ta có: \({S_1} = {S_{DCEF}} = DF \cdot CD \approx 0,62\left( {{\rm{\;}}{{\rm{m}}^2}} \right);{S_2} = {S_{ABNM}} = AB \cdot AM = 0,8\left( {{\rm{\;}}{{\rm{m}}^2}} \right)\).
Vậy thể tích phần nước trong bể là
\(V = \frac{1}{3} \cdot \left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right) \cdot AD = \frac{1}{3} \cdot \left( {0,62 + 0,8 + \sqrt {0,62 \cdot 0,8} } \right) \approx 0,71\left( {{\rm{\;}}{{\rm{m}}^3}} \right).\)
