
Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AD\).
a) Tính theo a thể tích khối chóp cụt \(AMN.A’B’D’\).
b) Tính theo a khoảng cách giữa hai đường thẳng \(MN\) và \(A’B\).

a) Tính theo a thể tích khối chóp cụt \(AMN.A’B’D’\).
Áp dụng công thức \(V = \frac{1}{3} \cdot AA’ \cdot \left( {{S_{AMN}} + {S_{A’B’D’}} + \sqrt {{S_{AMN}} \cdot {S_{A’B’D’}}} } \right)\)
b) Tính theo a khoảng cách giữa hai đường thẳng \(MN\) và \(A’B\).
- Tìm mặt phẳng chứa đường thẳng này và song song song với đường thẳng còn lại: \(MN//\left( {A’BD} \right)\)
- \(d\left( {MN,A’B} \right) = d\left( {MN,\left( {A’BD} \right)} \right) = d\left( {M,\left( {A’BD} \right)} \right) = \frac{1}{2}d\left( {A,\left( {A’BD} \right)} \right)\)
- Đặt \(h = d\left( {A,\left( {A’BD} \right)} \right)\) thì \(\frac{1}{{{h^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{A^{{\rm{‘}}2}}}} \Rightarrow \) \(h \Rightarrow \)\(d\left( {MN,A’B} \right) = d\left( {MN,\left( {A’BD} \right)} \right) = d\left( {M,\left( {A’BD} \right)} \right) = \frac{1}{2}d\left( {A,\left( {A’BD} \right)} \right)\)
Vậy \(d\left( {MN,A’B} \right) = d\left( {M,\left( {A’BD} \right)} \right) = \frac{{a\sqrt 3 }}{6}\).

Advertisements (Quảng cáo)
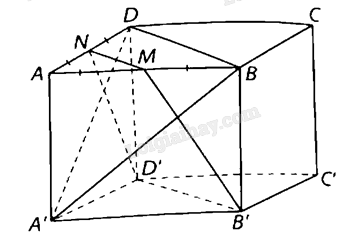
a) Ta có:
\({S_{A’B’D’}} = \frac{{{a^2}}}{2};{S_{AMN}} = \frac{{{a^2}}}{8};{S_{ABCD}} = {a^2};AA’ = a\), suy ra thể tích khối chóp cụt \(AMN \cdot A’B’D’\) là:
\(V = \frac{1}{3} \cdot AA’ \cdot \left( {{S_{AMN}} + {S_{A’B’D’}} + \sqrt {{S_{AMN}} \cdot {S_{A’B’D’}}} } \right)\)
\( = \frac{1}{3} \cdot a \cdot \left( {\frac{{{a^2}}}{8} + \frac{{{a^2}}}{2} + \sqrt {\frac{{{a^2}}}{8} \cdot \frac{{{a^2}}}{2}} } \right) = \frac{{7{a^3}}}{{24}}{\rm{.\;}}\)
b) Vì \(MN//BD\) nên \(MN//\left( {A’BD} \right)\), do đó:
\(d\left( {MN,A’B} \right) = d\left( {MN,\left( {A’BD} \right)} \right) = d\left( {M,\left( {A’BD} \right)} \right).\)
Vì \(M\) là trung điểm của \(AB\) nên \(d\left( {M,\left( {A’BD} \right)} \right) = \frac{1}{2}d\left( {A,\left( {A’BD} \right)} \right)\).
Đặt \(h = d\left( {A,\left( {A’BD} \right)} \right)\) thì \(\frac{1}{{{h^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{A^{{\rm{‘}}2}}}} = \frac{3}{{{a^2}}}\), suy ra \(h = \frac{{a\sqrt 3 }}{3}\).
Vậy \(d\left( {MN,A’B} \right) = d\left( {M,\left( {A’BD} \right)} \right) = \frac{{a\sqrt 3 }}{6}\).
