
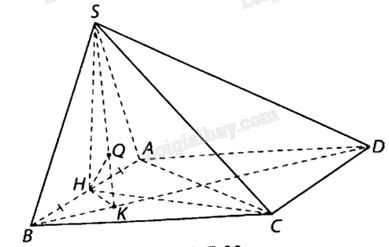
hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và \(SC = a\sqrt 2 \). Gọi H là trung điểm cạnh AB
a) Chứng minh rằng \(SH \bot (ABCD)\)
b) Tính theo \(a\) thể tích khối chóp \(S.ABCD\)
c) Tính theo \(a\) khoảng cách từ điểm A đến mặt phẳng \(\left( {SBD} \right)\)

Tính khoảng cách từ H đên (SBD), sau đó suy ra khoảng cách từ A đến (SBD)

Advertisements (Quảng cáo)
a) Ta có: \(SH = \frac{{a\sqrt 3 }}{2},HC = \frac{{a\sqrt 5 }}{2}\)
Suy ra \(S{H^2} + H{C^2} = S{C^2}\)
Do đó vuông tại H
Hay\(SH \bot HC\) lại có \(SH \bot AB\)
Nên \(SH \bot (ABCD)\)
b) ta có \(SH = \frac{{a\sqrt 3 }}{2},{S_{ABCD}} = {a^2}\)
Suy ra \({V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SH = \frac{1}{3}.{a^2}.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{6}\)
c) vì H là trung điểm của AB nên d(A, (SBD))=2.d(H,(SBD)). Kẻ HK vuông góc với BD tại K, HQ vuông góc với SK tại Q. Khi đó \(HQ \bot (SBD)\) suy ra d(H,(SBD))=HQ
ta tính được \(HK = \frac{{AC}}{4} = \frac{{a\sqrt 2 }}{4},SH = \frac{{a\sqrt 3 }}{4}\) mà tam giác SHK vuông tại H, đường cao HQ nên \(\frac{1}{{H{Q^2}}} = \frac{1}{{H{K^2}}} + \frac{1}{{H{S^2}}}\) suy ra \(HQ = \frac{{a\sqrt {21} }}{{24}}\), do đó d(A,(SBD))= \(HQ = \frac{{a\sqrt {21} }}{7}\)
