
Cho hình lăng trụ đứng \(ABC \cdot A’B’C’\) có \(\widehat {BAC} = {60^ \circ },AB = 2a,AC = 3a\) và số đo của góc nhị diện \(\left[ {A’,BC,A} \right]\) bằng \({45^ \circ }\).
a) Tính theo \(a\) khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {A’BC} \right)\).
b) Tính theo \(a\) thể tích khối lăng trụ \(ABC.A’B’C’\).

a) Tính theo a khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {A’BC} \right)\).
- Dựng \(AH\) vuông góc với \(BC\) tại \(H,AK\) vuông góc với \(A’H\) tại \(K\)
- Chứng minh \(AK \bot \left( {A’BC} \right)\), suy ra \(A’H \bot BC\).
- Góc nhị diện \(\left[ {A’,BC,A} \right]\) bằng \(\widehat {AHA’}\), suy ra \(\widehat {AHA’} = {45^ \circ }\) suy ra tam giác \(AHA’\)vuông cân.
- Theo định li côsin, áp dụng cho tam giác \(ABC\) tính \(BC\).
- \(AH = \frac{{2.{S_{ABC}}}}{{BC}} = \frac{{AB.AC.{\rm{sin}}\widehat {BAC}}}{{BC}}\).
- \(AK = \frac{1}{2}A’H\).
b) Tính theo a thể tích khối lăng trụ \(ABC \cdot A’B’C’\).
\({V_{ABC,A’B’C’}} = {S_{ABC}} \cdot AA’\)

Advertisements (Quảng cáo)
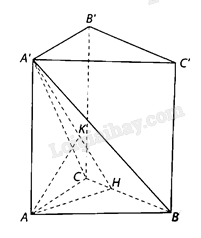
a) Kẻ \(AH\) vuông góc với \(BC\) tại \(H,AK\) vuông góc với \(A’H\) tại \(K\) thì \(AK \bot \left( {A’BC} \right)\), suy ra \(A’H \bot BC\).
Góc nhị diện \(\left[ {A’,BC,A} \right]\) bằng \(\widehat {AHA’}\), suy ra \(\widehat {AHA’} = {45^ \circ }\).
Theo định li côsin, áp dụng cho tam giác \(ABC\), ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2 \cdot AB.AC.{\rm{cos}}\widehat {BAC} = 7{a^2}\), suy ra \(BC = a\sqrt 7 \).
Do đó \(AH = \frac{{2.{S_{ABC}}}}{{BC}} = \frac{{AB.AC.{\rm{sin}}\widehat {BAC}}}{{BC}} = \frac{{3\sqrt {21} }}{7}a\).
Vì tam giác \(AHA’\) vuông cân tại \(A\) nên \(AK = \frac{{A’H}}{2} = \frac{{AH\sqrt 2 }}{2} = \frac{{3\sqrt {42} }}{{14}}a\).
Vậy \(d\left( {A,\left( {A’BC} \right)} \right) = \frac{{3\sqrt {42} }}{{14}}a\).
b) Thể tích khối lăng trụ \(ABC \cdot A’B’C’\) là \({V_{ABC,A’B’C’}} = {S_{ABC}} \cdot AA’ = \frac{1}{2} \cdot AB \cdot AC \cdot {\rm{sin}}{60^ \circ } \cdot AA’ = \frac{{27\sqrt 7 }}{{14}}{a^3}\)
