29. Trang 55 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện ABCD. Chứng minh rằng:
a) Các đoạn thẳng đi qua mỗi đỉnh và trọng tâm của mặt đối diện đồng quy tại một điểm G và điểm G chia trong mỗi đoạn thẳng đó theo tỉ lệ 3: 1 kể từ đỉnh đến trọng tâm của mặt đối diện.
b) Điểm G là trọng tâm của tứ diện ABCD.

a) Gọi A’, B’, C’, D’ lần lượt là trọng tâm của các tam giác BCD, CDA, ADB và ABC. Do A, B, C, D không đồng phẳng nên AA’, BB’, CC’, DD’ không đồng phẳng. Ta chứng minh các đoạn thẳng đó từng đôi một cắt nhau.
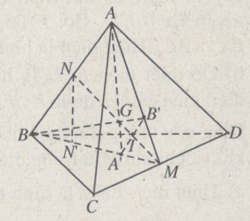
b) Gọi M’ là giao điểm của BA’ và CD. Khi đó M là trung điểm của CD. Vì B’ là trọng tâm của tam giác ACD nên ba điểm A, B’, M thẳng hàng. Vậy AA’ và BB’ cùng thuộc mp(ABM) và A’ thuộc đoạn BM, B’ thuộc đoạn AM nên AA’ và BB’ cắt nhau tại điểm G nào đó. Lí luận tương tự, ta cũng có các đường thẳng nói trên từng đôi cắt nhau. Vậy chúng phải đồng quy.
Ta có thể chứng minh cách khác như sau:
Lí luận như trên, trong tam giác ABM ta có AA’ và BB’ cắt nhau tại G. Vì
\({{A’M} \over {MB}} = {{B’M} \over {MA}} = {1 \over 3}\)
Advertisements (Quảng cáo)
Nên A’B’ // AB.
Suy ra: \({{GA’} \over {GA}} = {{GB’} \over {GB}} = {{A’B’} \over {AB}} = {{MA’} \over {MB}} = {1 \over 3}\)
Vậy \({{GA’} \over {GA}} = {{GB’} \over {GB}} = {1 \over 3}\)
Nhưng AA’, BB’ là hai đoạn thẳng tùy ý trong bốn đoạn thẳng AA’, BB’, CC’, DD’. Vậy chúng đồng quy tại điểm G và điểm G chia trong mỗi đoạn thẳng đó theo tỉ số 3: 1 kể từ đỉnh đến trọng tâm của mặt đối diện.
c) Nối M với G và kéo dài cắt AB tại N. Ta sẽ chứng minh N là trung điểm của AB và G là trung điểm của MN. Thật vậy, gọi I là giao điểm của MN với A’B’. Vì A’B’ // AB, ta có:
\({{IB’} \over {NB}} = {{GB’} \over {GB}} = {1 \over 3};\,\,{{IB’} \over {NA}} = {{MB’} \over {MA}} = {1 \over 3}\)
Nên \({{IB’} \over {NB}} = {{IB’} \over {NA}} \Rightarrow NB = NA\)
Suy ra N là trung điểm của AB.
Kẻ \(NN’/{\rm{AA}}’\,\,\left( {N’ \in BA’} \right)\)
Ta có N’ là trung điểm của BA’, suy ra A’ là trung điểm của N’M. Do đó A’G là đường trung bình của tam giác MNN’. Suy ra G là trung điểm của MN.
Vậy điểm G là trọng tâm của tứ diện ABCD.
