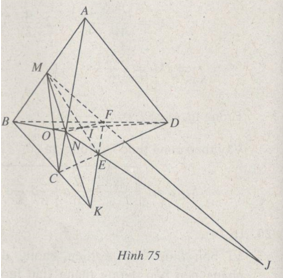
21. Trang 53 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện ABCD. Hai điểm M, N lần lượt nằm trên hai cạnh AB và AC sao cho \({{AM} \over {AB}} \ne {{AN} \over {AC}}.\) Một mặt phẳng (P) thay đổi luôn chứa MN, cắt các cạnh CD và BD lần lượt tại E và F.
a) Chứng minh rằng đường thẳng EF luôn đi qua một điểm cố định.
b) Tìm tập hợp giao điểm I của ME và NE.
c) TÌm tập hợp giao điểm J của MF và NE.

a) Gọi K là giao điểm của MN và BC thì K cố định và K là một điểm chung của mp(P) với mp(BCD). Mặt khác, \(mp\left( P \right) \cap mp\left( {BCD} \right) = EF\). Vậy K phải thuộc EF, nên EF luôn qua điểm cố định K.
Advertisements (Quảng cáo)
b) Ta có I là giao điểm của ME và NF. Vậy \(I \in ME,\,ME \subset \left( {MCD} \right) \Rightarrow I \in \left( {MCD} \right)\) và \(I \in NF,\,NF \subset \left( {NBD} \right) \Rightarrow I \in \left( {NBD} \right).\)
Từ đó, suy ra I thuộc giao tuyến OD của (MCD) và (NBD).
Khi E chạy đến C thì F chạy đến B và I chạy đến O.
Khi E chạy đến D thì F chạy đến D và I cũng chạy đến D.
Vậy tập hợp các điểm I là đoạn thẳng OD.
c) J là giao điểm của MF và NE. Từ đó dễ thấy J thuộc hai mặt phẳng (ABD) và (ACD). Vậy J phải thuộc giao tuyến AD của hai mặt phẳng (ABD) và (ACD).
Lí luận tương tự như câu a) ta thấy tập hợp các điểm J là đường thẳng AD trừ các điểm trong đoạn AD.
