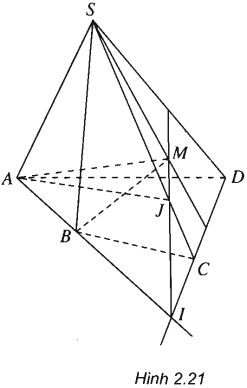
Cho hình chóp S.ABCDcó đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD.
Tìm giao tuyến của hai mặt phẳng
a) (SBM) và (SCD);
b) (ABM) và (SCD);
c) (ABM) và (SAC).

(h.2.21)
a) Ta có ngay S, M là hai điểm chung của (SBM) và (SCD) nên \(\left( {SBM} \right) \cap \left( {SC{\rm{D}}} \right) = SM\).
Advertisements (Quảng cáo)
b) M là điểm chung thứ nhất của (AMB) và (SCD)
Gọi \(I = AB \cap C{\rm{D}}\)
Ta có: \(I \in AB \Rightarrow I \in \left( {ABM} \right)\)
Mặt khác \(I \in C{\rm{D}} \Rightarrow I \in \left( {SC{\rm{D}}} \right)\)
Nên \(\left( {AMB} \right) \cap \left( {SC{\rm{D}}} \right) = IM\).
c) Gọi \(J = IM \cap SC\).
Tacó: \(J \in SC \Rightarrow J \in \left( {SAC} \right)\) và \(J \in IM \Rightarrow J \in \left( {ABM} \right)\).
Hiển nhiên \(A \in \left( {SAC} \right)\) và \(A \in \left( {ABM} \right)\)
Vậy \(\left( {SAC} \right) \cap \left( {ABM} \right) = AJ\)
