Cho hình chóp S.ABCDcó đáy là tứ giác ABCD. Gọi G1 và G1 lần lượt là trọng tâm của các tam giác SBC và SCD. Bài 2.48 trang 86 Sách bài tập (SBT) Hình học 11 - II. Đề toán tổng hợp
Cho hình chóp S.ABCDcó đáy là tứ giác ABCD. Gọi G1 và G1 lần lượt là trọng tâm của các tam giác SBC và SCD
Tìm giao tuyến của mặt phẳng (AG1G2) với các mặt phẳng (ABCD) và (SCD).
Xác định thiết diện của hình chóp với mặt phẳng (AG1G2).

Advertisements (Quảng cáo)
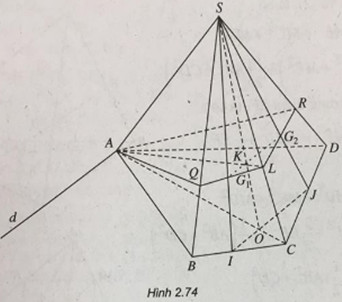
Gọi I, J lần lượt là trung điểm của BC, CD. Ta có \(IJ\parallel {G_1}{G_2}\) nên giao tuyến của hai mặt phẳng (AG1G2) và (ABCD) là đường thẳng d qua A và song song với IJ
Gọi \(O = IJ \cap AC,K = {G_1}{G_2} \cap SO,L = AK \cap SC\)
LG2 cắt SD tại R
LG2 cắt SB tại Q
Ta có thiết diện là tứ giác AQLR.
