Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gợi N, P, Q theo thứ tự là trung điểm của các cạnh BC, CC’, C’D’. Tìm diện tích thiết diện tạo bởi mặt phẳng (NPQ) cắt hình lập phương.

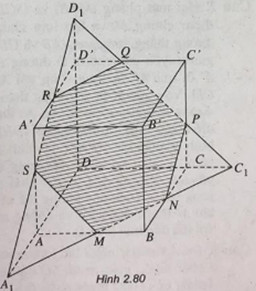
(h.2.80) Xác định thiết diện:
Trong mặt phẳng (DD’C’C), gọi \({C_1} = PQ \cap C{\rm{D, }}{{\rm{D}}_1} = PQ \cap DD’\)
Trong mặt phẳng (ABCD), gọi \(M = {C_1}N \cap AB,{A_1} = {C_1}N \cap A{\rm{D}}\)
Trong mặt phẳng (DD’A’A), gọi \(R = {D_1}{A_1} \cap A'{\rm{D’, S = }}{D_1}{A_1} \cap AA’\)
Ta có thiết diện cần tìm là lục giác MNPQRS
Advertisements (Quảng cáo)
+Tính diện tích thiết diện :
Các đỉnh của hình lục giác là trung điểm các cạnh của hình lập phương nên chúng bằng nhau và mỗi cạnh của lục giác bằng nửa đường chéo của hình vuông có cạnh bằng a.
Ta có: \(MN = NP = PQ = Q{\rm{R}} = R{\rm{S}} = SM = {{a\sqrt 2 } \over 2}\)
Ngoài ra \(\Delta {D_1}RQ = \Delta S{A_1}M = \Delta PN{C_1}\) ( chúng là những tam giác đều )
Suy ra: \(\widehat {SRQ} = \widehat {RQP} = \widehat {QPN} = \widehat {PNM} = \widehat {NMS} = \widehat {MSR} = {120^0}\)
Khi đó , ta có lục giác MNPQRS là lục giác đều.
\({S_{MNPQRS}} = {S_{{A_1}{C_1}{D_1}}} - 3{S_{{D_1}RQ}} = {{3{a^2}\sqrt 3 } \over 4}\).
