Cho hình chóp S.ABCD có đáy là hình thang ABCD (có đáy nhỏ BC). Gọi M, N lần lượt là trung điểm của AB và SD, O là giao điểm của AC và DM.. Bài 2.47 trang 86 Sách bài tập (SBT) Hình học 11 - II. Đề toán tổng hợp
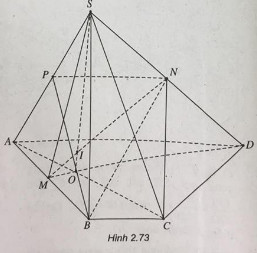
Cho hình chóp S.ABCD có đáy là hình thang ABCD (có đáy nhỏ BC). Gọi M, N lần lượt là trung điểm của AB và SD, O là giao điểm của AC và DM.
a) Tìm giao điểm của MN và mặt phẳng (SAC).
b) Tìm thiết diện của hình chóp với mặt phẳng (NBC). Thiết diện đó là hình gì?
Advertisements (Quảng cáo)
(h.2.73) a) Gọi \(O = AC \cap MD\). Trong mặt phẳng (SMB) gọi \(I = SO \cap MN\).
Ta có: \(I = \left( {SAC} \right) \cap MN\)
b) \(A{\rm{D}}\parallel BC\left( {BC \subset \left( {SBC} \right)} \right)\)
\( \Rightarrow A{\rm{D}}\parallel \left( {SBC} \right)\). Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến \(NP\parallel A{\rm{D}}\left( {P \in SA} \right)\). Ta có thiết diện cần tìm là hình thang BCNP.