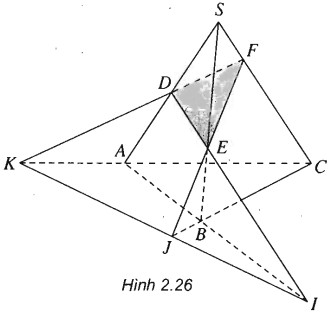
Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K.
Chứng minh ba điểm I, J, K thẳng hàng.
. Bài 2.7 trang 67 Sách bài tập (SBT) Hình học 11 - Bài 1. Đai cương về đường thằng và mặt phẳng
Chứng minh ba điểm I, J, K thẳng hàng.
. Bài 2.7 trang 67 Sách bài tập (SBT) Hình học 11 - Bài 1. Đai cương về đường thằng và mặt phẳng
Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K.
Chứng minh ba điểm I, J, K thẳng hàng.

(h.2.26)
Advertisements (Quảng cáo)
Ta có:
\(\eqalign{
& I = DE \cap AB \cr
& DE \subset \left( {DEF} \right) \Rightarrow I \in \left( {DEF} \right) \cr
& AB \subset \left( {ABC} \right) \Rightarrow I \in \left( {ABC} \right) \cr} \)
Lí luận tương tự thì J, K cũng lần lượt thuộc về hai mặt phẳng trên nên I, J, K thuộc về giao tuyến của (ABC) và (DEF) nên I, J, K thẳng hàng.
