Cho hình chóp tam giác S.ABC có \(SA = SB = SC = AB = AC = a\) và \(BC = a\sqrt 2 \). Tính góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \).

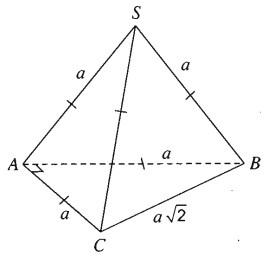
Ta tính côsin của góc giữa hai vectơ \(\overrightarrow {SC} \) và \(\overrightarrow {AB} \). Ta có
\(\eqalign{
& \cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {{\overrightarrow {SC} .\overrightarrow {AB} } \over {\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}} \cr
& = {{\left( {\overrightarrow {SA} + \overrightarrow {AC} } \right).\overrightarrow {AB} } \over {{a^2}}} = {{\overrightarrow {SA} .\overrightarrow {AB} + \overrightarrow {AC} .\overrightarrow {AB} } \over {{a^2}}} \cr} \)
Advertisements (Quảng cáo)
Theo giả thiết ta suy ra hình chóp có các tam giác đều là SAB, SAC và các tam giác vuông là ABC vuông tại A và SBC vuông tại S.
Do đó \(\overrightarrow {SA} .\overrightarrow {AB} = a.a.\cos 120^\circ = - {{{a^2}} \over 2}\) và \(\overrightarrow {AC} .\overrightarrow {AB} = 0\)
Vậy \(\cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {{ - {{{a^2}} \over 2} + 0} \over {{a^2}}} = - {1 \over 2}\)
Hay \(\left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {120^0}\)
Vậy góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} ) bằng 120°
