Chứng minh tứ giác A’B’CD là hình vuông.. Bài 3.14 trang 141 Sách bài tập (SBT) Hình học 11 - Bài 2. Hai đường thẳng vuông góc
Cho hình hộp thoi ABCD.A’B’C’D’ có tất cả các cạnh bằng a và \(\widehat {ABC} = \widehat {B’BA} = \widehat {B’BC} = {60^0}\). Chứng minh tứ giác A’B’CD là hình vuông.
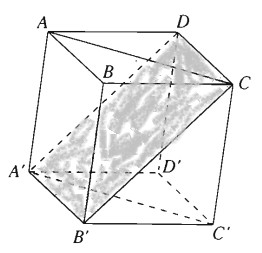
Advertisements (Quảng cáo)
Trước hết dễ thấy tứ giác A’B’CD là hình bình hành, ngoài ra \(B’C = a = C{\rm{D}}\) nên nó là hình thoi. Ta chứng minh hình thoi A’B’CD là hình vuông. Ta có:
\(\eqalign{
& \overrightarrow {CB’} .\overrightarrow {CD} = \left( {\overrightarrow {CB} + \overrightarrow {BB’} } \right).\overrightarrow {BA} \cr
& = \overrightarrow {CB} .\overrightarrow {BA} + \overrightarrow {BB’} .\overrightarrow {BA} \cr
& = - {{{a^2}} \over 2} + {{{a^2}} \over 2} = 0 \cr} \)
Vậy tứ giác A’B’CD là hình vuông.