Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a.. Bài 3.37 trang 162 Sách bài tập (SBT) Hình học 11 – Bài 5. Khoảng cách
Advertisements (Quảng cáo)
Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a.
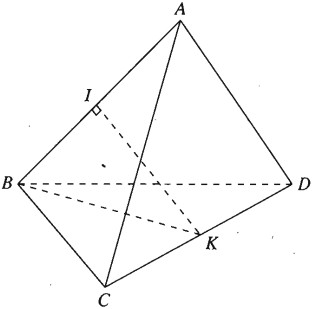
Giả thiết cho ABCD là tứ diện đều nên các cặp cạnh đối diện của tứ diện đó có vai trò như nhau. Do đó ta chỉ cần tính khoảng cách giữa hai cạnh AB và CD là đủ.
Gọi I và K lần lượt là trung điểm của AB và CD. Dễ thấy IK là đoạn vuông góc chung của AB và CD nên nó chính là khoảng cách giữa AB và CD.
Advertisements (Quảng cáo)
Tam giác BKI vuông tại I. Ta có :
\(I{K^2} = B{K^2} – B{I^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} – {\left( {{a \over 2}} \right)^2} = {{{a^2}} \over 2}\)
Vậy \(IK = {{a\sqrt 2 } \over 2}\).