
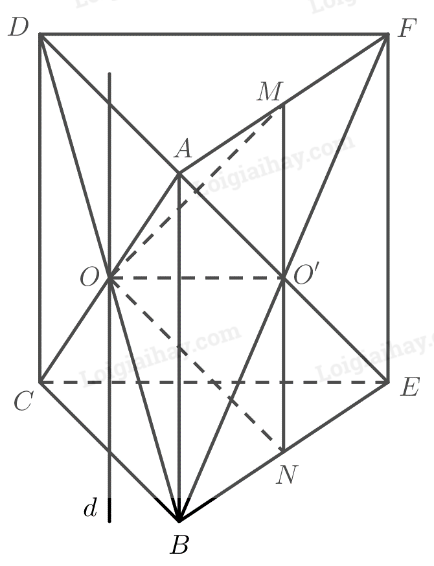
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không nằm trong cùng một mặt phẳng. Gọi \(O\) và \(O’\) lần lượt là tâm của \(ABCD\) và \(ABEF\).
a) Chứng minh đường thẳng \(OO’\) song song với các mặt phẳng \(\left( {CDF{\rm{E}}} \right),\left( {ADF} \right)\) và \(\left( {BCE} \right)\).
b) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AF\) và \(BE\). Chứng minh \(MN\parallel \left( {CDF{\rm{E}}} \right)\).
c) Tìm giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\).

– Để chứng minh đường thẳng song song với mặt phẳng, ta chứng minh đường thẳng đấy không nằm trong mặt phẳng và song song với một đường thẳng nằm trong mặt phẳng.
‒ Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách:
+ Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung.
+ Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó.

a) \(O\) là trung điểm của \(B{\rm{D}}\) (theo tính chất hình bình hành)
\(O’\) là trung điểm của \(BF\) (theo tính chất hình bình hành)
Advertisements (Quảng cáo)
\( \Rightarrow OO’\) là đường trung bình của tam giác \(B{\rm{D}}F\)
\(\left. \begin{array}{l} \Rightarrow OO’\parallel DF\\DF \subset \left( {C{\rm{DFE}}} \right)\end{array} \right\} \Rightarrow OO’\parallel \left( {C{\rm{DFE}}} \right)\)
Ta có:
\(\left. \begin{array}{l}OO’\parallel DF\\DF \subset \left( {A{\rm{DF}}} \right)\end{array} \right\} \Rightarrow OO’\parallel \left( {A{\rm{DF}}} \right)\)
\(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(O’\) là trung điểm của \(A{\rm{E}}\) (theo tính chất hình bình hành)
\( \Rightarrow OO’\) là đường trung bình của tam giác \(AC{\rm{E}}\)
\(\left. \begin{array}{l} \Rightarrow OO’\parallel CE\\CE \subset \left( {BCE} \right)\end{array} \right\} \Rightarrow OO’\parallel \left( {BC{\rm{E}}} \right)\)
b) \(M\) là trung điểm của \(AF\) (theo tính chất hình bình hành)
\(N\) là trung điểm của \(BE\) (theo tính chất hình bình hành)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABEF\)
\(\left. \begin{array}{l} \Rightarrow MN\parallel EF\parallel AB\\EF \subset \left( {C{\rm{D}}F{\rm{E}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {C{\rm{D}}F{\rm{E}}} \right)\)
Ta có:
\(\left. \begin{array}{l}O \in \left( {OMN} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN\parallel AB\\MN \subset \left( {OMN} \right)\\AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\}\)
\( \Rightarrow \)Giao tuyến của hai mặt phẳng \(\left( {OMN} \right)\) và \(\left( {ABCD} \right)\) là đường thẳng \(d\) đi qua \(O\), song song với \(MN\) và \(AB\).
