Hoạt động 1
Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.

Có nhận xét gì về giá trị của hàm số khi \(x\) càng gần đến 1?
b) Ở Hình 1, \(M\) là điểm trên đồ thị hàm số \(y = f\left( x \right)\); \(H\) và \(P\) lần lượt là hình chiếu của điểm \(M\) trên trục hoành và trục tung. Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) thay đổi như thế nào?
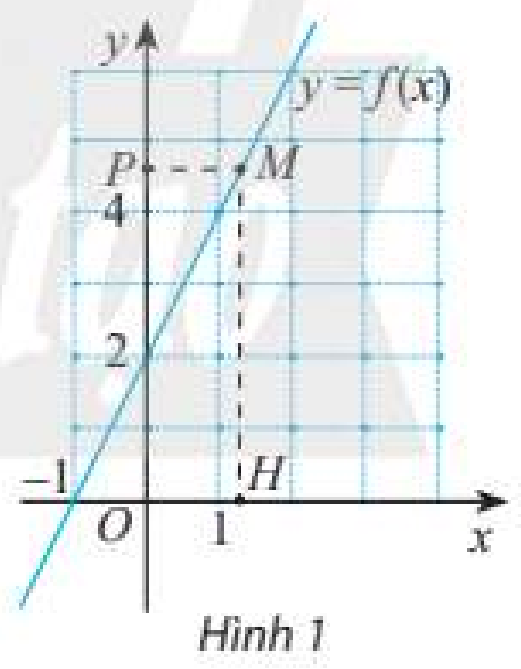

Quan sát đồ thị và nhận xét.

a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).
Thực hành 1
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right)\);
Advertisements (Quảng cáo)
b) \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}}\).

Đưa về tính giới hạn của dãy số \(\left( {{x_n}} \right)\) thỏa mãn \({x_n} \to {x_0}\) khi \(n \to + \infty \).

a) Đặt \(f\left( x \right) = 2{x^2} - x\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to 3\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \left( {2x_n^2 - {x_n}} \right) = 2.\lim x_n^2 - \lim {x_n} = {2.3^2} - 3 = 15\).
Vậy \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right) = 15\).
b) Đặt \(f\left( x \right) = \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to - 1\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \frac{{x_n^2 + 2{x_n} + 1}}{{{x_n} + 1}} = \lim \frac{{{{\left( {{x_n} + 1} \right)}^2}}}{{{x_n} + 1}} = \lim \left( {{x_n} + 1} \right) = \lim {x_n} + 1 = - 1 + 1 = 0\).
Vậy \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}} = 0\).
