Hoạt động 5
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
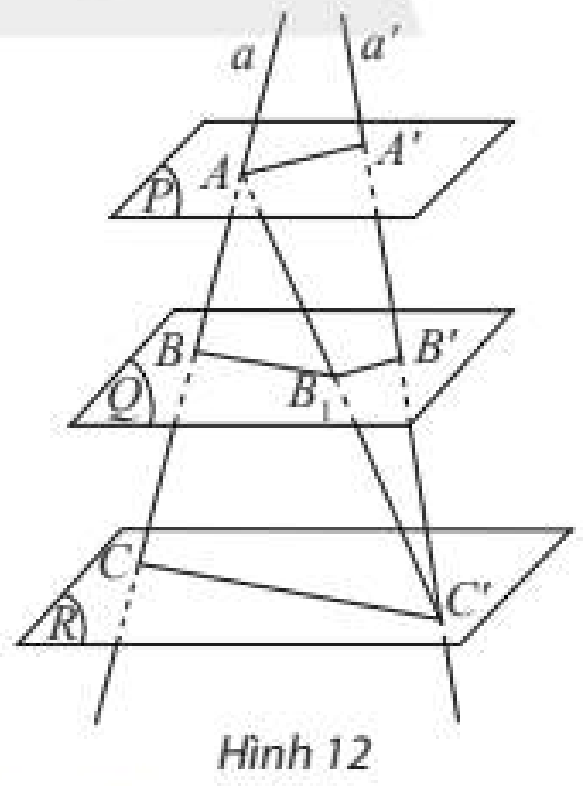
Cho ba mặt phẳng song song \(\left( P \right),\left( Q \right),\left( R \right)\) lần lượt cắt hai đường thăng \(a\) và \(a’\) tại các điểm \(A,B,C\) và \(A’,B’,C’\). Gọi \({B_1}\) là giao điểm của \(AC’\) với \(\left( Q \right)\) (Hình 12).
a) Trong tam giác \(ACC’\), có nhận xét gì về mối liên hệ giữa \(\frac{{AB}}{{BC}}\) và \(\frac{{A{B_1}}}{{{B_1}C’}}\)?
b) Trong tam giác \(AA’C’\), có nhận xét gì về mối liên hệ giữa \(\frac{{A{B_1}}}{{{B_1}C’}}\) và \(\frac{{A’B’}}{{B’C’}}\)?
c) Từ đó, nếu nhận xét về mối liên hệ giữa các tỉ số \(\frac{{AB}}{{A’B’}},\frac{{BC}}{{B’C’}},\frac{{AC}}{{A’C’}}\).

‒ Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
‒ Sử dụng định lí Thalès trong tam giác.
‒ Sử dụng tính chất của tỉ lệ thức.

a) Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( {ACC’} \right) \cap \left( Q \right) = B{B_1}\\\left( {ACC’} \right) \cap \left( R \right) = CC’\end{array} \right\} \Rightarrow B{B_1}\parallel CC’ \Rightarrow \frac{{AB}}{{BC}} = \frac{{A{B_1}}}{{{B_1}C’}}\left( 1 \right)\)
b) Ta có:
Advertisements (Quảng cáo)
\(\left. \begin{array}{l}\left( P \right)\parallel \left( Q \right)\\\left( {AA’C’} \right) \cap \left( Q \right) = B{B_1}\\\left( {AA’C’} \right) \cap \left( P \right) = AA’\end{array} \right\} \Rightarrow B{B_1}\parallel AA’ \Rightarrow \frac{{A{B_1}}}{{{B_1}C’}} = \frac{{A’B’}}{{B’C’}}\left( 2 \right)\)
c) Từ (1) và (2) suy ra \(\frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}} \Rightarrow \frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{AB + BC}}{{A’B’ + B’C’}} = \frac{{AC}}{{A’C’}}\)
Vậy \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{AC}}{{A’C’}}\).
Thực hành 3
Cho hình chóp \(S.ABC\) có \(SA = 9,SB = 12,SC = 15\). Trên cạnh \(SA\) lấy các điểm \(M,N\) sao cho \(SM = 4,MN = 3,N4 = 2\). Vẽ hai mặt phẳng song song với mặt phẳng \(\left( {ABC} \right)\), lần lượt đi qua \(M,N\), cắt \(SB\) theo thứ tự tại \(M’,N’\) và cắt \(SC\) theo thứ tự tại \(M”,N”\). Tính độ dài các đoạn thẳng \(SM’,M’N’,{\rm{ }}M”N”,N”C\).

Sử dụng định lí Thalès trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ.

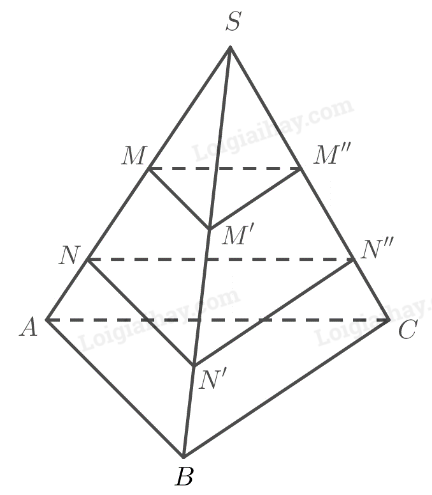
Ta có: \(\left( {MM’M”} \right)\parallel \left( {NN’N”} \right)\parallel \left( {ABC} \right)\) nên theo định lí Thalès ta có:
\(\frac{{SM}}{{SA}} = \frac{{SM’}}{{SB}} \Leftrightarrow SM’ = \frac{{SM.SB}}{{SA}} = \frac{{4.12}}{9} = \frac{{16}}{3}\)
\(\frac{{SA}}{{SB}} = \frac{{MN}}{{M’N’}} \Leftrightarrow M’N’ = \frac{{MN.SB}}{{SA}} = \frac{{3.12}}{9} = 4\)
\(\frac{{SA}}{{SC}} = \frac{{MN}}{{M”N”}} \Leftrightarrow M”N” = \frac{{MN.SC}}{{SA}} = \frac{{3.15}}{9} = 5\)
\(\frac{{SA}}{{SC}} = \frac{{NA}}{{N”C}} \Leftrightarrow N”C = \frac{{NA.SC}}{{SA}} = \frac{{2.15}}{9} = \frac{{10}}{3}\)
