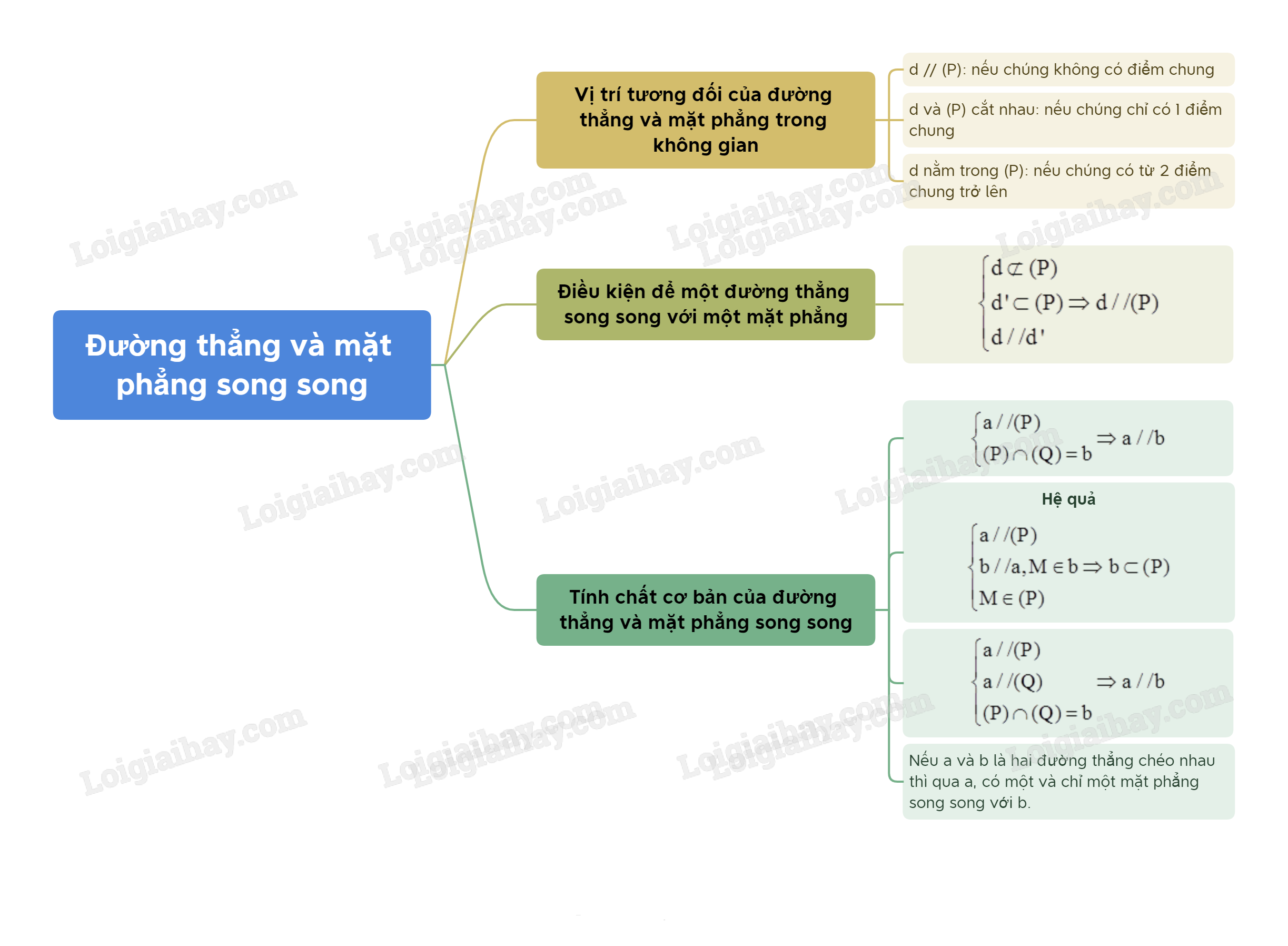
1. Đường thẳng song song với mặt phẳng
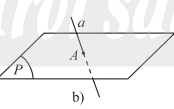
- Nếu a và \(\left( P \right)\) có một điểm chung duy nhất thì ta nói a và \(\left( P \right)\) cắt nhau tại A. Kí hiệu \(a \cap \left( P \right) = A\) hay \(a \cap \left( P \right) = \left\{ A \right\}\).
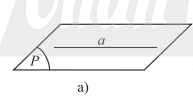
- Nếu a và \(\left( P \right)\) có từ 2 điểm chung phân biệt trở lên thì ta nói a nằm trong \(\left( P \right)\) hay \(\left( P \right)\) chứa a. Kí hiệu \(a \subset \left( P \right)\) hay \(\left( P \right) \supset a\).
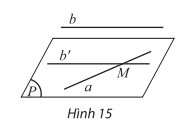
- Nếu a và \(\left( P \right)\) không có điểm chung thì ta nói a song song với \(\left( P \right)\) hay \(\left( P \right)\)song song với a. Kí hiệu là \(a//\left( P \right)\) hay \(\left( P \right)//a\).
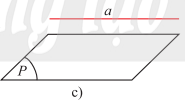
*Đường thẳng a song song với mặt phẳng (P) nếu chúng không có điểm chung.
2. Điều kiện để một đường thẳng song song với một mặt phẳng
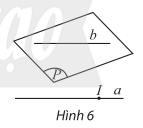
- Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì ta nói \(a//\left( P \right)\).
3. Tính chất cơ bản của đường thẳng và mặt phẳng song song
Advertisements (Quảng cáo)
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a // b.
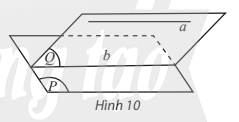
* Hệ quả:
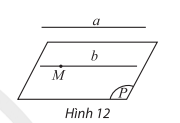
- Cho đường thẳng a song song với mặt phẳng (P). Nếu qua điểm M thuộc (P) ta vẽ đường thẳng b song song với a thì b phải nằm trong (P).
- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

* Mặt phẳng đi qua một trong hai đường thẳng chéo nhau và song song vơi đường thẳng còn lại
- Nếu a và b là hai đường thẳng chéo nhau thì qua a, có một và chỉ một mặt phẳng song song với b.