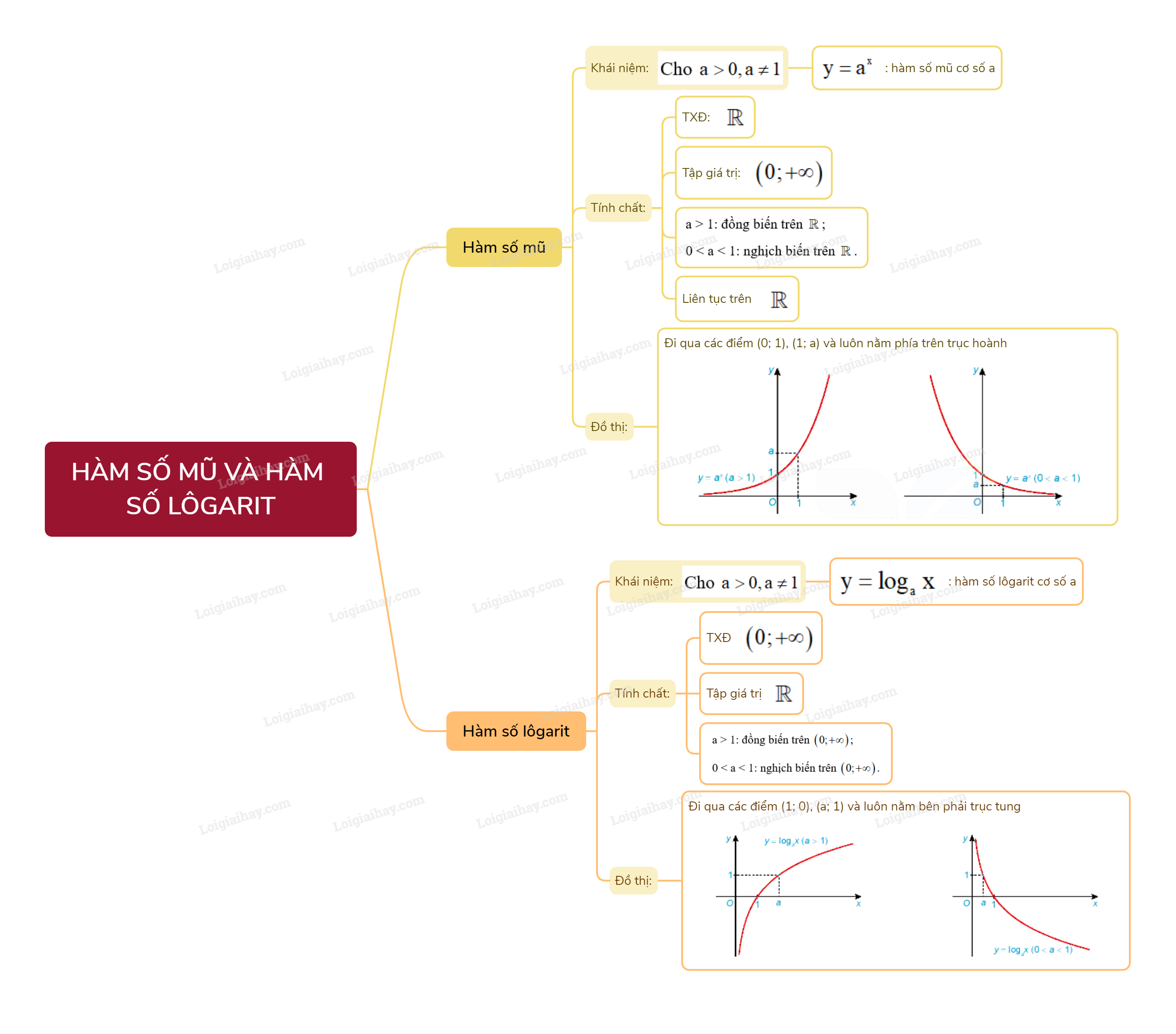
1. Hàm số mũ
a) Khái niệm hàm số mũ
Cho a là số thực dương khác 1.
Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a.
b) Đồ thị và tính chất của hàm số mũ
Hàm số mũ \(y = {a^x}\):
- Có tập xác định là \(\mathbb{R}\) và tập giá trị là \(\left( {0; + \infty } \right)\);
- Đồng biến trên \(\mathbb{R}\) khi a > 1 và nghịch biến trên \(\mathbb{R}\) khi 0 < a < 1;
- Liên tục trên \(\mathbb{R}\);
- Có đồ thị đi qua các điểm (0; 1), (1; a) và luôn nằm phía trên trục hoành.
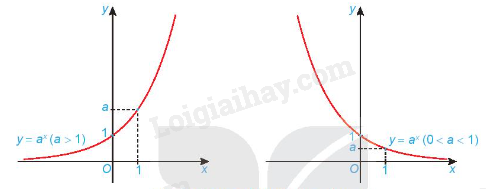
Dạng đồ thị của hàm số \(y = {a^x}\)
Advertisements (Quảng cáo)
2. Hàm số lôgarit
a) Khái niệm hàm số lôgarit
Cho a là số thực dương khác 1.
Hàm số \(y = {\log _a}x\) được gọi là hàm số lôgarit cơ số a.
b) Đồ thị và tính chất của hàm số lôgarit
Hàm số lôgarit \(y = {\log _a}x\):
- Có tập xác định là \(\left( {0; + \infty } \right)\) và tập giá trị là \(\mathbb{R}\);
- Đồng biến trên \(\left( {0; + \infty } \right)\) khi a > 1 và nghịch biến trên \(\left( {0; + \infty } \right)\) khi 0 < a < 1;
- Có đồ thị đi qua các điểm (1; 0), (a; 1) và luôn nằm bên phải trục tung.
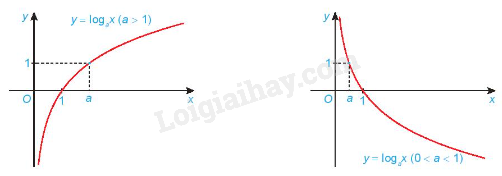
Dạng đồ thị của hàm số \(y = {\log _a}x\)