Bài 10. Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình \(y = {x \over 3}\) với đồ thị của hàm số \(y = \sin x\) đều cách gốc tọa độ một khoảng nhỏ hơn \(\sqrt {10} \)

Đường thẳng \(y = {x \over 3}\) đi qua các điểm \(E(-3 ; -1)\) và \(F(3 ; 1)\)
Advertisements (Quảng cáo)
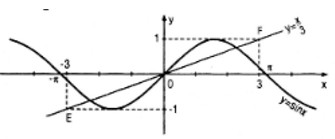
Chỉ có đoạn thẳng \(EF\) của đường thẳng đó nằm trong dải \(\left\{ {\left( {x{\rm{ }};{\rm{ }}y} \right)| - 1{\rm{ }} \le {\rm{ }}y{\rm{ }} \le {\rm{ }}1} \right\}\) (dải này chứa đồ thị cuả hàm số \(y = \sin x\)). Vậy các giao điểm của đường thẳng \(y = {x \over 3}\) với đồ thị của hàm số \(y = \sin x\) phải thuộc đoạn \(EF\) ; mọi điểm của đoạn thẳng này cách \(O\) một khoảng dài hơn \(\sqrt {9 + 1} = \sqrt {10} \) (và rõ ràng \(E, F\) không thuộc đồ thị của hàm số \(y = \sin x\)).
